一、基于sigmoid函数的logistic回归
import numpy as np class LogisticRegression: def __init__(self, n_iter=200, eta=1e-3, tol=None): # 训练迭代次数 self.n_iter = n_iter # 学习率 self.eta = eta # 误差变化阈值 self.tol = tol # 模型参数w(训练时初始化) self.w = None def _z(self, X, w): ‘‘‘g(x)函数: 计算x与w的内积.‘‘‘ return np.dot(X, w) def _sigmoid(self, z): ‘‘‘Logistic函数‘‘‘ return 1. / (1. + np.exp(-z)) def _predict_proba(self, X, w): ‘‘‘h(x)函数: 预测y为1的概率.‘‘‘ z = self._z(X, w) return self._sigmoid(z) def _loss(self, y, y_proba): ‘‘‘计算损失‘‘‘ m = y.size p = y_proba * (2 * y - 1) + (1 - y) return -np.sum(np.log(p)) / m def _gradient(self, X, y, y_proba): ‘‘‘计算梯度‘‘‘ return np.matmul(y_proba - y, X) / y.size def _gradient_descent(self, w, X, y): ‘‘‘梯度下降算法‘‘‘ # 若用户指定tol, 则启用早期停止法. if self.tol is not None: loss_old = np.inf self.loss_list = [] # 使用梯度下降至多迭代n_iter次, 更新w. for step_i in range(self.n_iter): # 预测所有点为1的概率 y_proba = self._predict_proba(X, w) # 计算损失 loss = self._loss(y, y_proba) self.loss_list.append(loss) print(‘%4i Loss: %s‘ % (step_i, loss)) # 早期停止法 if self.tol is not None: # 如果损失下降不足阈值, 则终止迭代. if loss_old - loss < self.tol: break loss_old = loss # 计算梯度 grad = self._gradient(X, y, y_proba) # 更新参数w w -= self.eta * grad def _preprocess_data_X(self, X): ‘‘‘数据预处理‘‘‘ # 扩展X, 添加x0列并置1. m, n = X.shape X_ = np.empty((m, n + 1)) X_[:, 0] = 1 X_[:, 1:] = X return X_ def train(self, X_train, y_train): ‘‘‘训练‘‘‘ # 预处理X_train(添加x0=1) X_train = self._preprocess_data_X(X_train) # 初始化参数向量w _, n = X_train.shape self.w = np.random.random(n) * 0.05 # 执行梯度下降训练w self._gradient_descent(self.w, X_train, y_train) def predict(self, X): ‘‘‘预测‘‘‘ # 预处理X_test(添加x0=1) X = self._preprocess_data_X(X) # 预测y=1的概率 y_pred = self._predict_proba(X, self.w) # 根据概率预测类别 return np.where(y_pred >= 0.5, 1, 0)
二、基于梯度下降的softmax回归
import numpy as np class SoftmaxRegression: def __init__(self, n_iter=200, eta=1e-3, tol=None): # 训练迭代次数 self.n_iter = n_iter # 学习率 self.eta = eta # 误差变化阈值 self.tol = tol # 模型参数W(训练时初始化) self.W = None def _z(self, X, W): ‘‘‘g(x)函数: 计算x与w的内积.‘‘‘ if X.ndim == 1: return np.dot(W, X) return np.matmul(X, W.T) def _softmax(self, Z): ‘‘‘softmax函数‘‘‘ E = np.exp(Z) if Z.ndim == 1: return E / np.sum(E) return E / np.sum(E, axis=1, keepdims=True) def _predict_proba(self, X, W): ‘‘‘h(x)函数: 预测y为各个类别的概率.‘‘‘ Z = self._z(X, W) return self._softmax(Z) def _loss(self, y, y_proba): ‘‘‘计算损失‘‘‘ m = y.size p = y_proba[range(m), y] return -np.sum(np.log(p)) / m def _gradient(self, xi, yi, yi_proba): ‘‘‘计算梯度‘‘‘ K = yi_proba.size y_bin = np.zeros(K) y_bin[yi] = 1 return (yi_proba - y_bin)[:, None] * xi def _stochastic_gradient_descent(self, W, X, y): ‘‘‘随机梯度下降算法‘‘‘ # 若用户指定tol, 则启用早期停止法. if self.tol is not None: loss_old = np.inf end_count = 0 # 使用随机梯度下降至多迭代n_iter次, 更新w. m = y.size idx = np.arange(m) for step_i in range(self.n_iter): # 计算损失 y_proba = self._predict_proba(X, W) loss = self._loss(y, y_proba) print(‘%4i Loss: %s‘ % (step_i, loss)) # 早期停止法 if self.tol is not None: # 随机梯度下降的loss曲线不像批量梯度下降那么平滑(上下起伏), # 因此连续多次(而非一次)下降不足阈值, 才终止迭代. if loss_old - loss < self.tol: print(‘haha‘) end_count += 1 if end_count == 5: break else: end_count = 0 loss_old = loss # 每一轮迭代之前, 随机打乱训练集. np.random.shuffle(idx) for i in idx: # 预测xi为各类别概率 yi_proba = self._predict_proba(X[i], W) # 计算梯度 grad = self._gradient(X[i], y[i], yi_proba) # 更新参数w W -= self.eta * grad def _preprocess_data_X(self, X): ‘‘‘数据预处理‘‘‘ # 扩展X, 添加x0列并置1. m, n = X.shape X_ = np.empty((m, n + 1)) X_[:, 0] = 1 X_[:, 1:] = X return X_ def train(self, X_train, y_train): ‘‘‘训练‘‘‘ # 预处理X_train(添加x0=1) X_train = self._preprocess_data_X(X_train) # 初始化参数向量W k = np.unique(y_train).size _, n = X_train.shape self.W = np.random.random((k, n)) * 0.05 # 执行随机梯度下降训练W self._stochastic_gradient_descent(self.W, X_train, y_train) def predict(self, X): ‘‘‘预测‘‘‘ # 预处理X_test(添加x0=1) X = self._preprocess_data_X(X) # 对每个实例计算向量z. Z = self._z(X, self.W) # 向量z中最大分量的索引即为预测的类别. return np.argmax(Z, axis=1)
三、加载数据集
数据集的下载网址是
http://archive.ics.uci.edu/ml/machine-learning-databases/wine/
import numpy as np X=np.genfromtxt(‘F:/python_test/data/wine.data‘,delimiter=‘,‘,usecols=range(1,14)) print(X) print(X.shape)

y=np.genfromtxt(‘F:/python_test/data/wine.data‘,delimiter=‘,‘,usecols=0) print(y)

四、测试二分类模型——logistic模型
数据处理,删除数据集中为3的部分,并且将是1和2的部分-1
#删除数据集中为3的部分,并且将是1和2的部分-1 index=y!=3 X=X[index] y=y[index] y-=1 print(‘样本集:\n‘,X) print(‘结果集:\n‘,y)

加载模型和划分数据集
clf=LogisticRegression(n_iter=2000,eta=0.01,tol=0.0001) from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
查看属性的均值以及方差,以防梯度下降过程对于属性存在偏向,发现存在差异后通过z标准化处理之后将训练集以及测试集都转化成标准化数据
print(X.mean(axis=0)) print(X.var(axis=0)) from sklearn.preprocessing import StandardScaler ss=StandardScaler() #使用训练数据去获取期望以及方差 ss.fit(X_train)

X_train_std=ss.transform(X_train) X_test_std=ss.transform(X_test) print(X_train_std[:3]) print(X_test_std[:3])
训练模型,668次迭代之后误差值收敛,这里的损失函数是对极大似然函数改变符号之后除以样本空间的大小,所以求极大似然函数的最大值与求loss函数的最小值是等价的。
clf.train(X_train_std,y_train)
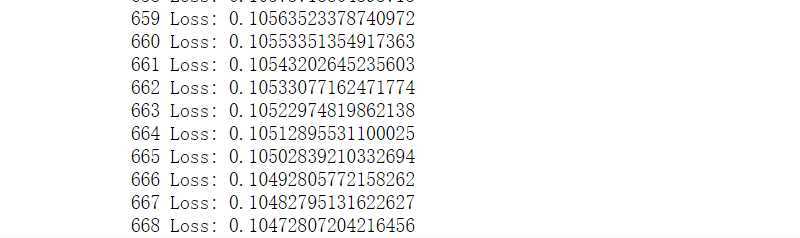
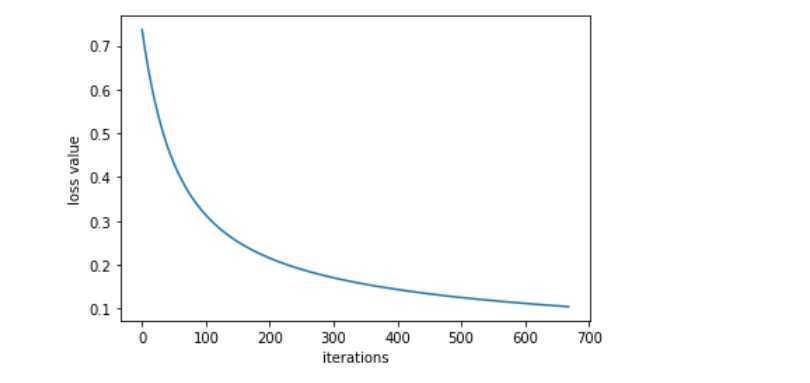
损失函数在668次迭代中的变化曲线
import matplotlib.pyplot as plt plt.plot(clf.loss_list) plt.xlabel(‘iterations‘) plt.ylabel(‘loss value‘) plt.show()
测试并且计算出精度以及多次测试求平均的精确度
from sklearn.metrics import accuracy_score y_pred=clf.predict(X_test_std) accuracy_rate=accuracy_score(y_test,y_pred) print(accuracy_rate)
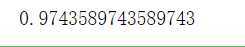
def test(X,y): X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) ss=StandardScaler() ss.fit(X_train) X_train_std=ss.transform(X_train) X_test_std=ss.transform(X_test) clf=LogisticRegression(n_iter=2000,eta=0.01,tol=0.0001) clf.train(X_train_std,y_train) y_pred=clf.predict(X_test_std) accuracy = accuracy_score(y_test,y_pred) return accuracy accuracy_mean=np.mean([test(X,y) for _ in range(50)]) print(accuracy_mean)
求得平均精确度是0.9764102564102565
五、测试Softmax多分类回归模型
获取数据集,这里注意需要将分类变量从float64变成int64类型,因为代码中有将分类变量作为index传到np.ndarray中去,float类型会出错,必须使用bool或者是int类型的数据
并且需要将转化之后的ndarray复制回去
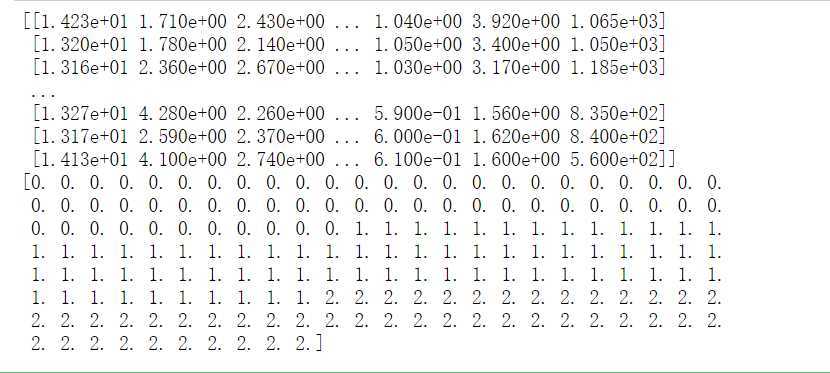
import numpy as np X=np.genfromtxt(‘F:/python_test/data/wine.data‘,delimiter=‘,‘,usecols=range(1,14)) y=np.genfromtxt(‘F:/python_test/data/wine.data‘,delimiter=‘,‘,usecols=0) #将数据变成0,1,2分类 y-=1 y=y.astype(‘int64‘) print(X) print(y) print(type(X)) print(y.dtype)
构建分类器、划分数据、训练模型
clf=SoftmaxRegression(n_iter=2000,eta=0.01,tol=0.0001) from sklearn.model_selection import train_test_split X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3) from sklearn.preprocessing import StandardScaler ss=StandardScaler() ss.fit(X_train)
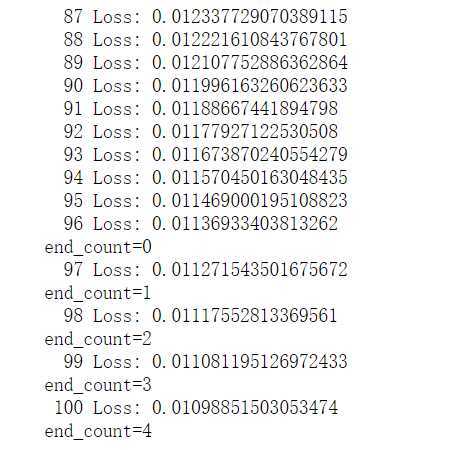
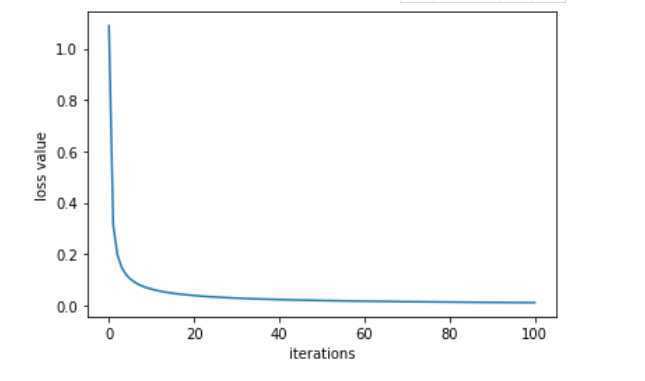
100次迭代收敛,损失函数曲线绘制如下
X_train_std=ss.transform(X_train)
X_test_std=ss.transform(X_test)
clf.train(X_train_std,y_train)
import matplotlib.pyplot as plt plt.plot(clf.loss_list) plt.xlabel(‘iterations‘) plt.ylabel(‘loss value‘) plt.show()
测试平均准确度
def test(X,y): X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3) ss=StandardScaler() ss.fit(X_train) X_train_std=ss.transform(X_train) X_test_std=ss.transform(X_test) clf=SoftmaxRegression(n_iter=2000,eta=0.01,tol=0.0001) clf.train(X_train_std,y_train) y_pred=clf.predict(X_test_std) accuracy = accuracy_score(y_test,y_pred) return accuracy accuracy_mean=np.mean([test(X,y) for _ in range(50)]) print(accuracy_mean)
得到平均准确度是0.9774074074074073
机器学习:logistic回归与Softmax回归 代码+案例
原文:https://www.cnblogs.com/randy-lo/p/13210429.html