南大周志华老师在 2010 年提出一个异常检测算法 Isolation Forest,在工业界很实用,算法效果好,时间效率高,能有效处理高维数据和海量数据,这里对这个算法进行简要总结。
提到森林,自然少不了树,毕竟森林都是由树构成的,看 Isolation Forest(简称 iForest)前,我们先来看看 Isolation Tree(简称 iTree)是怎么构成的,iTree 是一种随机二叉树,每个节点要么有两个女儿,要么就是叶子节点,一个孩子都没有。给定一堆数据集 D,这里 D 的所有属性都是连续型的变量,iTree 的构成过程如下:

iTree 构建好了后,就可以对数据进行预测啦,预测的过程就是把测试记录在 iTree 上走一下,看测试记录落在哪个叶子节点。iTree 能有效检测异常的假设是:异常点一般都是非常稀有的,在 iTree 中会很快被划分到叶子节点,因此可以用叶子节点到根节点的路径 h(x) 长度来判断一条记录 x 是否是异常点;对于一个包含 n 条记录的数据集,其构造的树的高度最小值为 log(n),最大值为 n-1,论文提到说用 log(n) 和 n-1 归一化不能保证有界和不方便比较,用一个稍微复杂一点的归一化公式:
,
??(??,??)s(x,n)就是记录 x 在由 n 个样本的训练数据构成的 iTree 的异常指数,??(??,??)s(x,n)取值范围为 [0,1],越接近 1 表示是异常点的可能性高,越接近 0 表示是正常点的可能性比较高,如果大部分的训练样本的 s(x,n) 都接近于 0.5,说明整个数据集都没有明显的异常值。
随机选属性,随机选属性值,一棵树这么随便搞肯定是不靠谱,但是把多棵树结合起来就变强大了;
iTree 搞明白了,我们现在来看看 iForest 是怎么构造的,给定一个包含 n 条记录的数据集 D,如何构造一个 iForest。iForest 和 Random Forest 的方法有些类似,都是随机采样一一部分数据集去构造每一棵树,保证不同树之间的差异性,不过 iForest 与 RF 不同,采样的数据量??????Psi不需要等于 n,可以远远小于 n,论文中提到采样大小超过 256 效果就提升不大了,明确越大还会造成计算时间的上的浪费,为什么不像其他算法一样,数据越多效果越好呢,可以看看下面这两个个图,
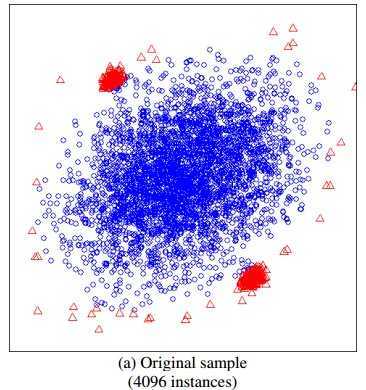
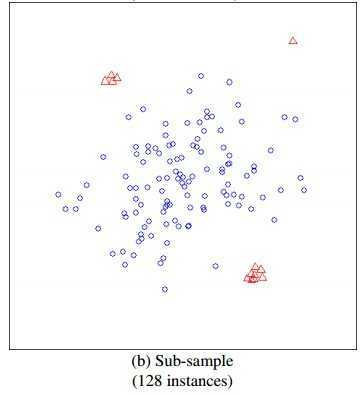
左边是元素数据,右边是采样了数据,蓝色是正常样本,红色是异常样本。可以看到,在采样之前,正常样本和异常样本出现重叠,因此很难分开,但我们采样之和,异常样本和正常样本可以明显的分开。
除了限制采样大小以外,还要给每棵 iTree 设置最大高度??=??????????????(??????Ψ2)l=ceiling(log2Ψ),这是因为异常数据记录都比较少,其路径长度也比较低,而我们也只需要把正常记录和异常记录区分开来,因此只需要关心低于平均高度的部分就好,这样算法效率更高,不过这样调整了后,后面可以看到计算?(??)h(x)需要一点点改进,先看 iForest 的伪代码:

IForest 构造好后,对测试进行预测时,需要进行综合每棵树的结果,于是
??(?(??))E(h(x))表示记录 x 在每棵树的高度均值,另外 h(x) 计算需要改进,在生成叶节点时,算法记录了叶节点包含的记录数量,这时候要用这个数量????????Size估计一下平均高度,h(x) 的计算方法如下:

在处理高维数据时,可以对算法进行改进,采样之后并不是把所有的属性都用上,而是用峰度系数 Kurtosis 挑选一些有价值的属性,再进行 iTree 的构造,这跟随机森林就更像了,随机选记录,再随机选属性。
这个算法本质上是一个无监督学习,不需要数据的类标,有时候异常数据太少了,少到我们只舍得拿这几个异常样本进行测试,不能进行训练,论文提到只用正常样本构建 IForest 也是可行的,效果有降低,但也还不错,并可以通过适当调整采样大小来提高效果。
全文完,转载请注明出处:http://www.cnblogs.com/fengfenggirl/p/iForest.html
全文完
原文:https://www.cnblogs.com/cx2016/p/13211288.html