1.基本定理的验证
代码如下:
from sympy import * A, B, C = symbols(‘A B C‘) # 重叠律 # A·A=A A+A=A print(to_cnf(A | A)) print(to_cnf(A & A)) # 结合律 print(to_cnf(~(A | B) | C)) # 分配律 # A+B·C=(A+B)(A+C) print(to_dnf(A & (B | C))) # 反演律 print(to_dnf(~(A | B))) print(to_dnf(~(A & B))) # 还原律 print(to_cnf(~(~A)))
运行结果:

2.化简逻辑函数
代码如下:
from sympy import * A, B, C = symbols(‘A B C‘) # 化简逻辑函数(!A+!B+!C)(!A+!B+!C) f1 = simplify_logic((~A & ~B & ~C) | (~A & ~B & C)) print(f1) # 化简最小项之和为析取范式 minterms1 = [0, 7] f2 = SOPform([A, B, C], minterms1) print(f2) # 化简最小项之和为合取范式 minterms2 = [[1, 0, 1], [1, 1, 0], [1, 1, 1]] f3 = POSform([A, B, C], minterms2) print(f3) # 化简最小项之和为析取范式(第7项任取) minterms3 = [[1, 0, 1], [1, 1, 0]] dontcares = [7] f4 = SOPform([A, B, C], minterms3, dontcares) print(f4)
运行结果:
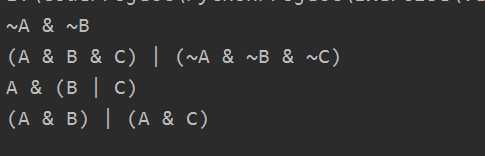
原文:https://www.cnblogs.com/wanyuan/p/13210134.html