每个人的思路不同,自然思考时遇到的困难那就不同,我这里仅仅是记录了自己思考过程中的困难以及理解思路,所以叙事的详略也只是根据我个人的思路而言,至于能否帮到读者就不好说了,当然我还是希望我的解释过程能对你的理解产生帮助。文章内容部分来源网络,仅当作个人备忘。
拟阵是一个满足如下条件的序偶 M = (S , I)
1. S是一个有限集
2. I 是S的子集的一个非空集族,这些子集称为S的独立子集,使得如果B∈I,且A包含于B,则A∈I,如果I满足此性质,则称之为遗传的。空集必然是I的成员
3. 如果A∈I,B∈I 且A比B元素数更少,那么存在某个元素x属于B-A使得A∪{x}∈I,则称拟阵M满足交换性质
(关于第三条交换性的个人理解:拟阵具有膨胀性,总是可以膨胀(或者说,扩展)成为极大独立集,这能解释为什么给定一个拟阵,这个拟阵中的所有基,具有同样的大小)
下面以图拟阵为例进行分析,首先给出图拟阵的概念
首先给出图拟阵的定义
图拟阵(记为M_G = S_G , I_G)定义在一个给定的无向图G = (V , E)上,满足下列条件
1. S_G定义为 E,也就是G的边集
2. A 是 E 的子集,则A ∈ I_G 当且仅当A是无圈的。换而言之,A是独立的当且仅当G_A形成一个森林
结合图拟阵说明拟阵的三条性质
首先非空有限集,显然边集S_G满足条件
其次遗传性,考虑B ∈ I,且A包含于B。A,B根据定义,显然是森林,森林的自己也还是森林,所以A ∈ I 也成立,遗传性得证
最后考虑交换性,我们按照性质构造两个森林,分别记作A和B,他们的顶点集相同,这里不妨假设B比A包含有更多的边,于是,计算他们连通块的个数,根据图论里的公式,连通块个数 = 点数 - 边数(可以自己画个图感受一下,三个点,一条边,两个分量),于是B由于边更多,所以连通块数量就更少,整体上感受就是B是整块的,而A更加零碎
更进一步,一定会有 B 中的一条边 e 连接 A 中的两个分量。可以这么来理解,A和B一人拿一个连通块,B总是尽可能地不让自己的块包含两个A的块,怎么做,很简单,跟A选择一样的块就行了,这样直到B耗尽了自己所有的块,它仍然一直保持着没有链接两个A的小块,但是由于它的块数更少,无法继续进行操作了。
现在考虑A,A为了增加自己的连通块数应该怎么做?任何链接两个连通块的操作都会降低连通块个数,例如连接两个点,所以A只能将自己已经存在的连通块进行拆分,而这样,我们的假设也就得证了,因为此时在A中被破坏的边,不正是我们要找的链接A中两个分量的边吗?
这样我们就找到了一条边e,它来自B的边集,连接了A的两个连通块,根据森林的性质,把两个数合并为一个树自然是不会生成圈的,此时的A∪{e} 仍然是满足图拟阵的性质的,交换性得证
上述分析过程可以看出,一个序偶是否为拟阵,我们的主要目标是证明其是否具有交换性,而一般的思路也是构造两个大小不同的序偶,将其中较大序偶中的一个独有的元素,一般称之为边,加入另一个较小的序偶中,接下来只需要考察这个序偶+新加入的边是否仍然满足集族的性质即可。
这里涉及到了另一种拟阵,线性拟阵,简而言之就是一组基底,我们在研究线性拟阵的时候实际上实在研究对应的矩阵的性质,类似的,如果定义一个矩阵M,它可以用列向量来表示拟阵 M = (S , I) 中S的每一个边,那么我们就称此拟阵 M 是可表出的,矩阵M为其表出
简单说,判断一个拟阵能不能被表出,问能不能找到一个矩阵,使得矩阵的列向量的独立性能和拟阵的独立性对应起来。
证明:首先我们对一个图G构造矩阵M,首先对无向图的每一条边随意赋予一个方向,对于这个有向边,记为e = (u , v) 对于除了u v以外的所有分量,也就是与它无关的其他节点,我们都赋值0,对于节点u我们赋值为1,与之相对v赋值为-1。这样,问题就等价为证明矩阵M上的列向量是线性无关(即,可表出),当且仅当这组向量表示的边集是无圈的 (即,是图拟阵)
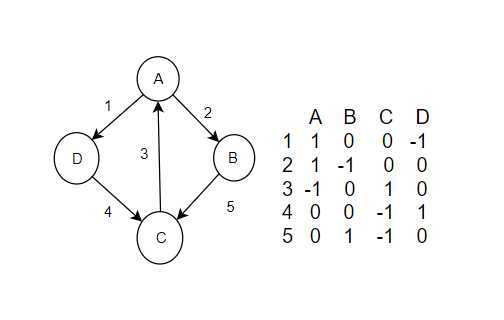
上图展示了如何用向量表示图
先证必要性,假设图中是包含圈的,我们对于这个圈C上的每一条边e都让他对应到一个值a,当我们按照顺序遍历这个圈上的所有边是,如果它的方向和我们便=遍历的方向相反,我们将这个值赋值为-1,反之如果同方向则赋值为+1,这样,对于这个圈上的每一个点,他都出现了两次,一次进一次出,这时,我们对这个圈上的所有边乘上我们刚刚赋的值a,求和结果一定是0,这就跟线性无关这个条件矛盾了,所以图中无圈
再证充分性,同样反证,假设我们得到的向量组不满足线性无关,同样假设每条边对应一个值a,既然不独立,那么必然会有一组非零的a使得v*a求和结果为零,队与那些a≠0的边集,至少有一个点之链接了一条边,而这就是的v*a求和结果不可能为零,矛盾,所以得到的向量组满足线性无关。
证明结论过程中,我们没有用到任何对条件的假设,所以我们可以得出结论,任何域下,图拟阵都是可以表出的。
很多可以用贪心算法得到最优解的问题都可以形式化为在一个加权拟阵中寻找最大权重独立子集的问题
下面为了证明整个过程通过贪心法选出的最大权重解的确是整个问题的最优解
引理4.1
假设M = (S , I) 是一个加权拟阵,加权函数为 w ,且已经按照权值进行排序,令x是 S 中第一个满足 { x } 独立的元素,如果存在这样的 x ,那么存在S的一个最优解子集 A 包含 x。
这个引理是什么意思?我们为何要先证明这个引理?因为贪心选择性的定义就是若一个问题的全局最优解可以通过局部最优解得到,那么称其具有贪心选择性。这就要求我们通过归纳法进行证明。而这个引理就是作为递归基础的!所以必须先证明之。
引理4.1证明
假设不存在这样的 x 那么唯一的独立子集就是空集,满足引力;若存在这样的 x,则假设一个同样是最优子集的 B 存在且不包含 x ,因为如果包含 x ,那我们就不用证了
现在我们构造一个子集 A ,初始时只包含 x ,即 A = { x } ,由于拟阵具有交换性,我们可以不断地从 B 中选出新元素加入 A ,而且由于 { x } 是满足独立性的,A将始终保持独立性,直到 | A | = | B |,这时,A B二者之间唯一的差别就在A 中包含x,而B中不包含x而包含一个别的元素y,由于x是第一个满足独立性的元素且处于最大权值队列的队首,所以x的权重必然 ≧ y的权值,因为B是最优子集,所以A也是最优子集,因为A至少不会比B更差。这样我们的引理就证明完毕,也就确保了拟阵贪心选择性证明的归纳基础。以此为基础,我们可以进行迭代调用。
现在又有一个问题,x是怎么选出来的?那些没选的边是应该继续放回队列吗?
引理4.2
M = (S , I) 是一个拟阵,如果 x 是 S 中的一个元素,而且是S的某个独立子集A的一个扩展,则x也是空集的一个扩展
这个引理的目的性并不明确,先证明出来一会再研究
引理4.2证明
由于x是A的扩展,可知A∪{x}是独立的,根据遗传性,{x}也是独立的,所以x是空集的一个扩展
推论4.3
M = (S , I) 是一个拟阵,如果 x 是 S 中的一个元素,如果x不是空集的扩展,那么他也不是S的任意独立子集A的一个扩展
这个推论是不是感觉有点意思?没错,证明上面那个不知所以的引理就是为了证明这个推论。推论指出,任何元素如果在首次出现时不能用于构造独立集,那他之后永远都不可能被用到了。换句话说,如果一个元素在初始时不是最优,那他随后也不会被加入到最优解集合中。
这就使得我们需要在构建最优解的过程中,每一步都选择当前的最优解而无需考虑其他子问题,贪心选择性得证。
引理4.4
M = (S , I) 是一个拟阵,如果 x 是 S 中通过贪心法选择出的的第一个元素,那么接下来寻找包含x的最大权重独立子集的问题转化为寻找 M’ = (S’ , I‘) 的最大权重独立子集的问题
用剪枝法证明,如果子问题不是最优的则可以通过剪切的方式得到一个更好的解
结论 拟阵上的贪心算法具有正确性
参考文章链接:https://zhuanlan.zhihu.com/p/54072907
参考教材:算法导论(第三版)第16章
原文:https://www.cnblogs.com/owczhlol/p/13219771.html