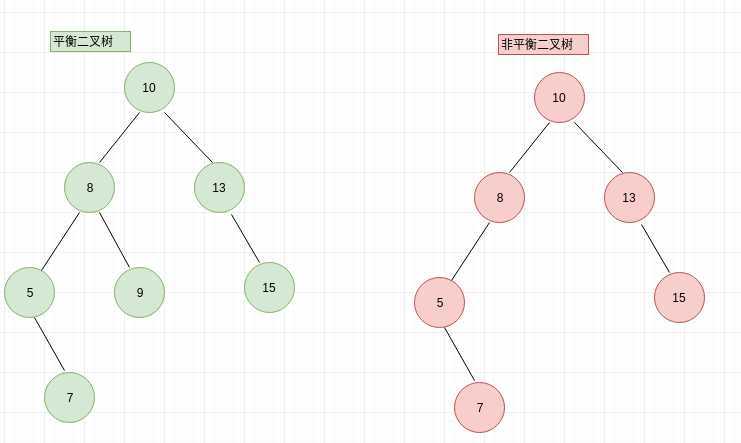
(1) AVL树本质上还是一棵二叉搜索树,
1.本身首先是一棵二叉搜索树。
2.带有平衡条件:每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
也就是说,AVL树,本质上是带了平衡功能的二叉查找树(二叉排序树,二叉搜索树)。
(2)平衡因子
节点的左右子树高度差
(1)节点基础设计
public class AvlTree<T extends Comparable<T>> { class Node{ T t; Node left; Node right; int height; public Node(T t) { this.t=t; height=1; left=null; right=null; } } private Node root; //获取节点高度 public int getHeight(Node current) { if(current==null) { return 0; } return current.height; } //获取节点平衡因子 public int getBalanceFactor(Node current) { if(current==null) { return 0; } return getHeight(current.left)-getHeight(current.right); } //前序遍历 public void preTraversal(Node current) { if(current!=null) { System.out.println(current.t); preTraversal(current.left); preTraversal(current.right); } } //判断是否是平衡二叉树 public boolean isBalanced(Node current) { if(current==null) { return true; } int balanceFactory=Math.abs(getBalanceFactor(current)); if(balanceFactory>1) { return false; } return isBalanced(current.left)&&isBalanced(current.right); } }
(2)添加、删除节点时可能会导致二叉树不平衡,为了保持平衡 LL(右旋)、RR(左旋) LR(先左旋、右旋) RL(先右旋、左旋)
(a)LL(右旋)
LL表示新增或者删除节点之后,节点的平衡因子大于1,且左孩子的平衡因子大于0,形成如下x-->y-->z的形式,需要右旋操作才能保持平衡。
如下图:插入、删除节点之后二叉树就会不平衡,此时应该相应的旋转,使二叉树达到平衡。
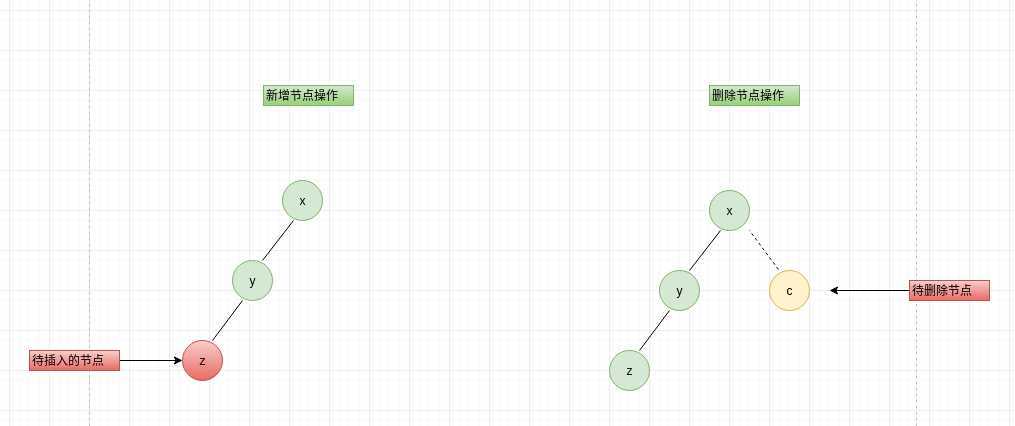
上图插入删除之后如下:
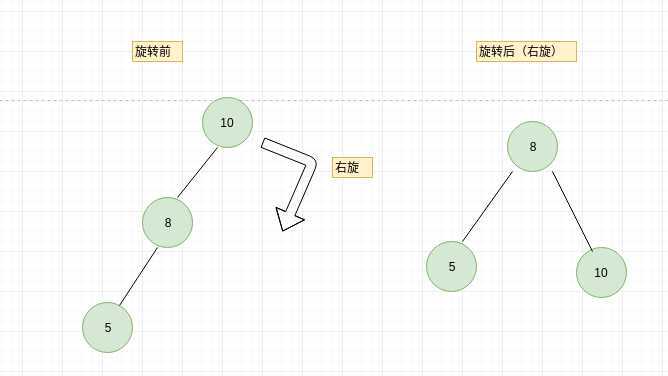
右旋操作抽象分析,便于代码实现,分析图如下:
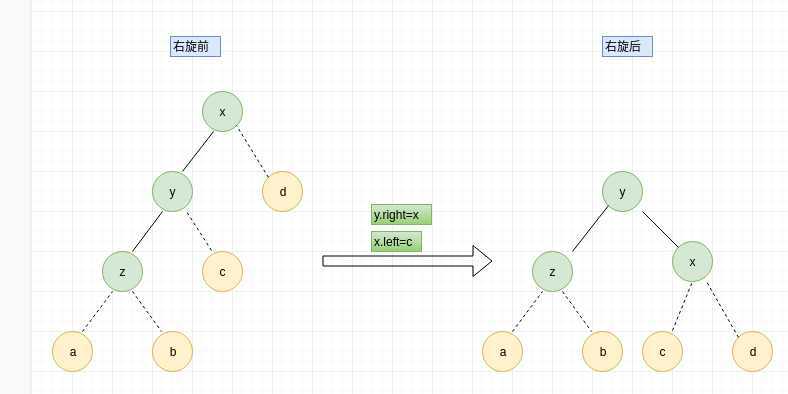
右旋操作代码实现:
//右旋 /* x y * * y d ----------> z x * * z c a b c d * * a b */ public Node rightRotate(Node x) { Node y=x.left; Node c=y.right; y.right=x; x.left=c; //更新树的高度 添加节点的时候每个节点的高度会自动刷新(递归调用) y.height=Math.max(getHeight(y.left),getHeight(y.right))+1; x.height=Math.max(getHeight(y.left),getHeight(y.right))+1; return y; }
(b)RR左旋
RR是向节点的右孩子的右子树新增节点或者删除节点的左孩子,使节点的平衡因子小于-1,节点右孩子平衡因子小于0,形成x-->y--z靠右形式
导致节点不平衡,此时需要左旋,使其平衡。
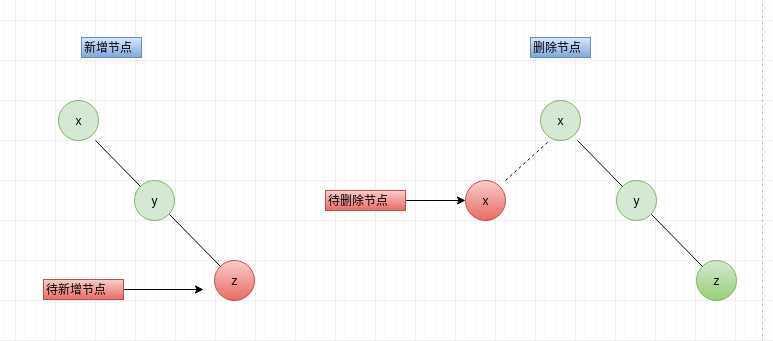
左旋操作:
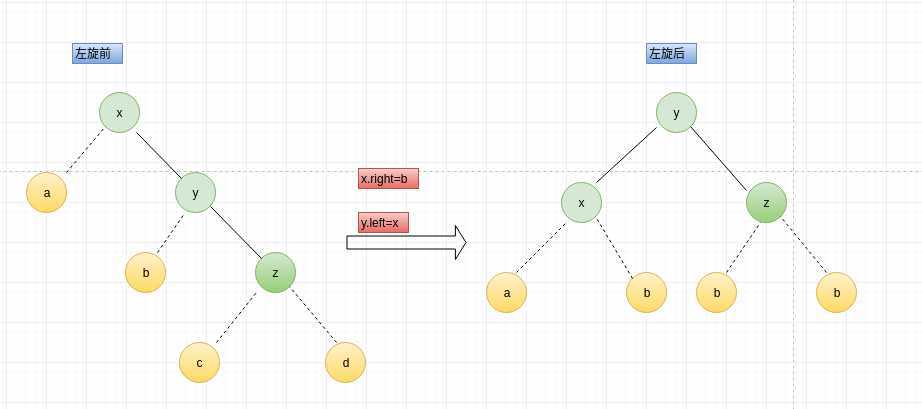
源代码如下:
//左旋 /* * x y * * a y -------> x z * * d z a d */ public Node leftRotate(Node x) { Node y=x.right; Node d=y.left; y.left=x; x.right=d; //更新高度 新增节点时候、递归每个节点高度会刷新 y.height=Math.max(getHeight(y.left),getHeight(y.right))+1; x.height=Math.max(getHeight(y.left),getHeight(y.right))+1; return y; }
(c)LR、先左旋形成LL再右旋。
LR意思节点平衡因子大于1,且节点左孩子的平衡因子小于0,新增、删除节点时形成如下图x-->y-->z,需左旋再右旋
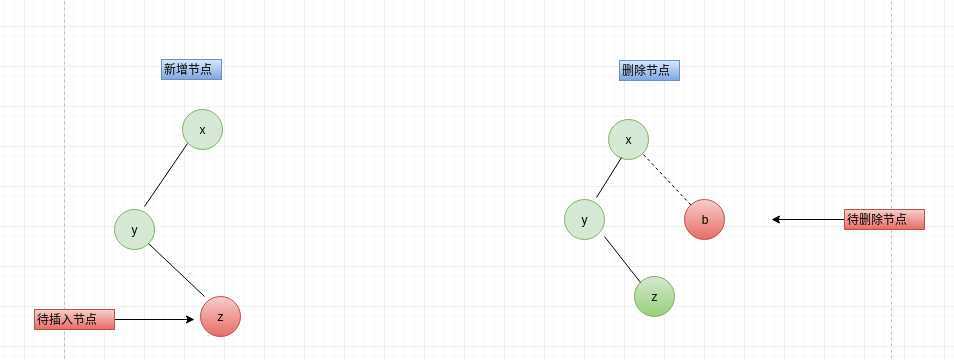
先左旋、再右旋实现过程如下:
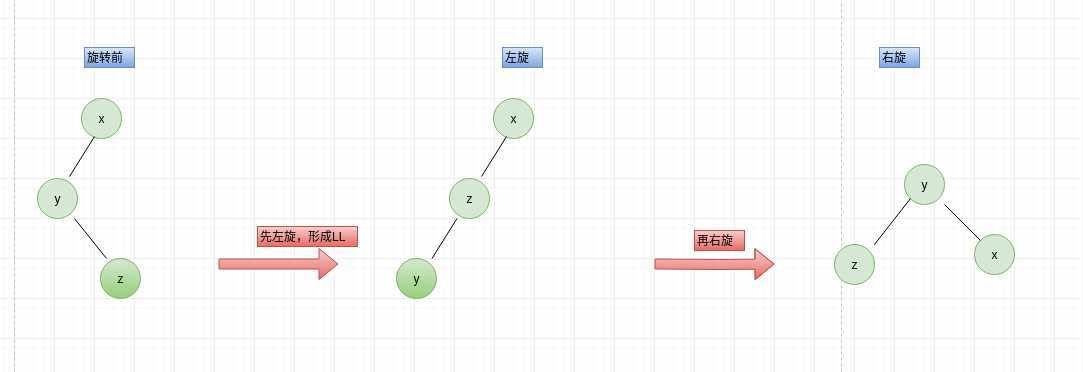
代码入下:
/*LR 先左旋再右旋
* x x z
* 左旋 右旋
* y ----> z -------> y x
*
* z y
*
* x代表current
*/
if(balanceFactor>1&&getBalanceFactor(current.left)<0) {
current.left=leftRotate(current.left);
return rightRotate(current);
}
(d)、RL先右旋形成形成RR再左旋达到平衡
RL的意思当前节点的平衡因子小于-1,节点的右孩子的平衡因子大于0,形成如下x-->y-->z,如下图:
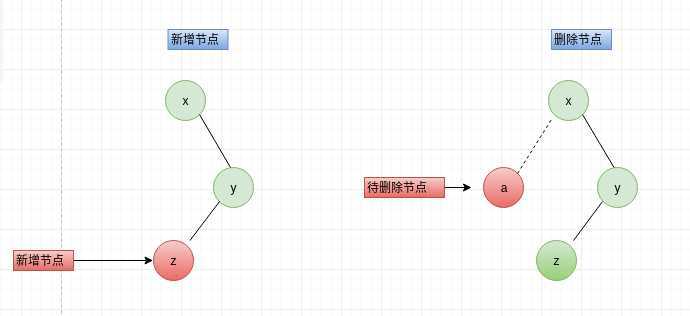
先右旋、再左旋实现过程如下:
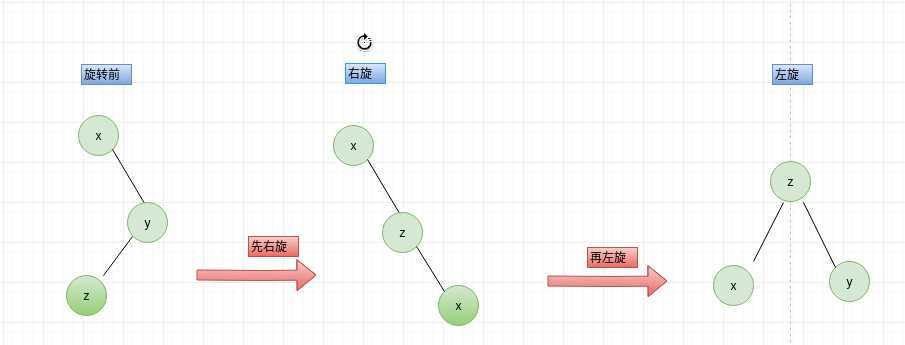
代码如下:
/*RL 先右旋再左旋 * x x z * 右旋 左旋 * y ------> z ----> x y * * z y * x代表crrent */ if(balanceFactor<-1&&getBalanceFactor(current.right)>0) { current.right=rightRotate(current.right); return leftRotate(current); }
(3)节点新增操作源码如下:
public void addNode(T t) { root=addNode(root,t); } public Node addNode(Node current,T t) { if(current==null) { return new Node(t); } if(t.compareTo(current.t)<0) { current.left=addNode(current.left,t); }else if(t.compareTo(current.t)>0) { current.right=addNode(current.right,t); } //更新节点高度、递归到的都会更新 current.height=1+Math.max(getHeight(current.left), getHeight(current.right)); //平衡因子 int balanceFactor=getBalanceFactor(current); /*LL 右旋操作 * * x * * y * * z */ if(balanceFactor>1&&getBalanceFactor(current.left)>0) { return rightRotate(current); } /*RR 左旋操作 * x * * y * * z */ if(balanceFactor<-1&&getBalanceFactor(current.right)<0) { return leftRotate(current); } /*LR 先左旋再右旋 * x x z * 左旋 右旋 * y ----> z -------> y x * * z y * * x代表current */ if(balanceFactor>1&&getBalanceFactor(current.left)<0) { current.left=leftRotate(current.left); return rightRotate(current); } /*RL 先右旋再左旋 * x x z * 右旋 左旋 * y ------> z ----> x y * * z y * x代表crrent */ if(balanceFactor<-1&&getBalanceFactor(current.right)>0) { current.right=rightRotate(current.right); return leftRotate(current); } return current; }
测试新增节点如下:正常二叉树插入10 8 6 4 5 ,前序遍历结果就是10 8 6 4 5,但AVL树遍历结果应该是8 5 4 6 10
public static void main(String[] args) { AvlTree<Integer> avlTree=new AvlTree<Integer>(); avlTree.addNode(10); avlTree.addNode(8); avlTree.addNode(6); avlTree.addNode(4); avlTree.addNode(5); avlTree.preTraversal(avlTree.root); }
AVl树测试结果如下:
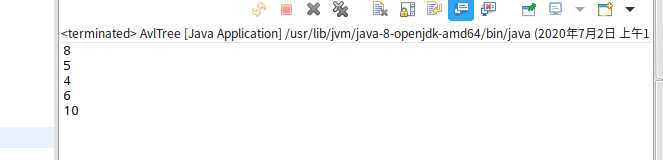
(4)节点删除操作源码如下
原文:https://www.cnblogs.com/kjcc/p/13217578.html