资料参考
题外话
scratchapixel的文章都很不错,缺点是稍啰嗦,啃起来比较慢。
老外的教程都是怕别人看不懂,一个概念用2种方法说2遍的那种。
下面是总结:
首先我们先来判断一个点在直线的左边还是右边
设直线起点和终点分别是p0和p1,点为p
我们用p1-p0 得到直线的向量 \(\vec l\)
用p-p0得到关于p点的向量 \(\vec p\)
然后对2个向量使用叉乘:
\(\vec l \times \vec p\)
利用2d向量的叉乘性质,在右手坐标系中
如果点p在直线的右边,叉乘结果>0
如果点p在直线的左边,叉乘结果<0
如果点p在直线上,叉乘结果=0
对三角形来说,利用这个原理,对三角形的三条边分别叉乘
如果三个结果都>0或者都<0,则点在三角形内部
以下是对scratchapixel关于点在三角形内部判断的节选翻译:
之前已经提到过,得到点是否和三角形重合有多重方法。列出更古老的方法确实是个不错的主意,不过这个课程中,我们只说明当今最普遍的方法。这个方法被Juan Pineda 在1988年的论文《"A Parallel Algorithm for Polygon Rasterization》中被提出。
在我们开始细究Pineda的技术之前,我们先描述一下算法的原理。我们可以说,一个三角形的边可以看做是一条把一个2d平面分成2个部分的直线。Pineda的算法的原理是找到一个函数,他称之为边界函数,这样我们可以测试给定一个点在直线的哪一边(图二的点p)。点在直线的左边,则这个函数返回负数,右边返回正数,恰好在直线上则返回0。
原文的图2
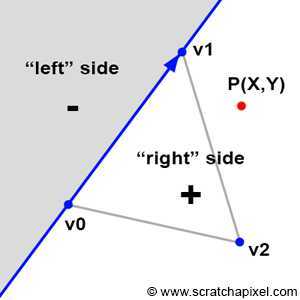
在图2中,我们用这个函数对三角形的第一条边(用顶点v0和v1定义。注意2者的先后顺序非常重要)进行检测。如果我们对另外2条边也用相同的方法,我们可以清晰的看到一个区域(白色部分),这个区域内的所有点都是正值(图3)
原文的图3
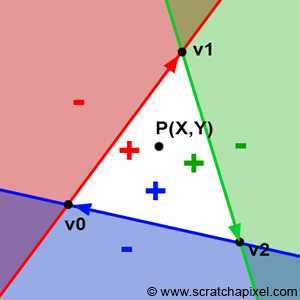
如果我们取这个区域内的任意一点,我们就能发现,这个点位均为于三条边的右侧。如果P是在一个像素中心的一个点,我们就可以使用这个方法判断像素是否和三角形重叠。假设对于这个点,我们发现三角形的所有三条边均返回正值,那么该像素被三角形包含(或者与某条边重合)。Pinada 的这个方法正巧是线性的,这就意味着这个方法可以被增量计算,这一点我们待会再讲。
既然我们已经理解了原理,让我们揭示下这个函数是什么。边界函数被定义为(边界用顶点v0和v1来定义):
未完待续...
原文:https://www.cnblogs.com/terrynoya/p/13226339.html