【核心算法9】分治算法

分治算法的核心思想是将一个规模很大的问题化简为n个规模较小的问题，这些子问题虽然独立而不同，但是问题的本质是一致的，从而达到分而治之的目的

• 归并排序
• 连续子列表的最大和
• 几何问题-凸包
• 数学问题-多项式乘法

归并排序

归并排序是一种有效的排序算法。其他常见的八种排序算法包括冒泡排序，插入排序，二叉树排序，快速排序，堆排序，希尔排序等

问题描述

将乱序的数列用归并算法将其排序输出

思路描述

归并算法有两种类型：递归法(Top-down) 和迭代法(Bottom-up)

递归法描述

递归法的核心思想是

1. 把列表分为两个子列表，单独排序子列表再合并子列表。

2. 如图，递归法可以利用二叉树理解：列表为根节点，子列表为子节点。

   

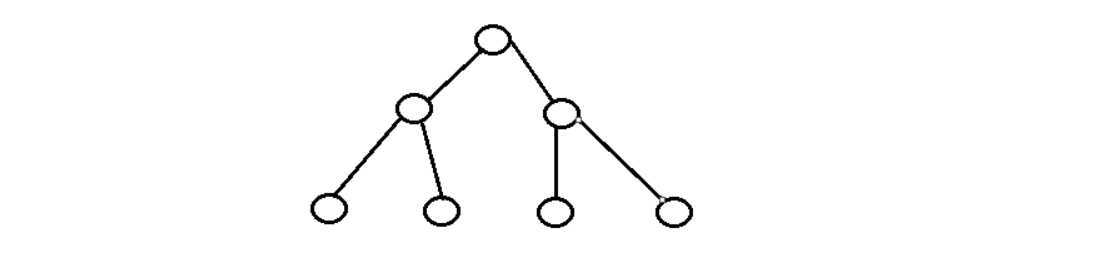
3. 首先排序子列表，再一步步合并子列表

这个算法之所以称为递归法是因为它利用递归的思想，把根节点的问题递给子节点，一环套一环解决问题

迭代法描述

迭代法的核心思想是

1. 利用for循环将列表的子列表成对排序合并，最后组成一个整体

2. 如图，迭代法可以利用倒二叉树：对独立子列表(子节点) 进行多次迭代，直到完整列表(根节点)

   

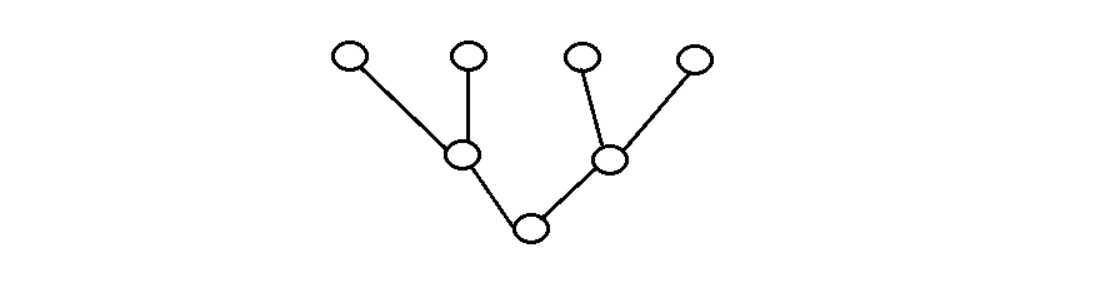
3. 首先把列表看成n个长度为1的子列表，利用循环把相邻的两个子列表合并

4. 得到 n/2 个长度为2的子列表

5. 依次类推，最后得到长度为n的完整列表

代码实现

递归法

def merge_sort1(arr):
    """
    递归法 归并排序
    :param arr: 乱序数组
    :return: 
    """
    if len(arr) < 2:
        return
    # 找到列表中点
    cut = len(arr) // 2
    # 左子列表
    arr1 = arr[: cut]
    # 右子列表
    arr2 = arr[cut: ]
    # 左子列表归并排序
    merge_sort1(arr1)
    # 右子列表归并排序
    merge_sort1(arr2)

    pointer1 = 0
    pointer2 = 0
    counter = 0
    while pointer1 < len(arr1) and pointer2 < len(arr2):
        if arr1[pointer1] < arr2[pointer2]:
            arr[counter] = arr1[pointer1]
            pointer1 += 1
        else:
            arr[counter] = arr2[pointer2]
            pointer2 += 1
        counter += 1
    while pointer1 < len(arr1):
        arr[counter] = arr1[pointer1]
        pointer1 += 1
        counter += 1
    while pointer2 < len(arr2):
        arr[counter] = arr2[pointer2]
        pointer2 += 1
        counter += 1
        
array = [2, 3, 4, 1, -2, 0, 5, 1]
merge_sort1(array)
print(array)

# >>>

迭代法

def merge_sort2(arr):
    length = len(arr)
    n = 1
    while n < length:
        for i in range(0, length, n*2):
            arr1 = arr[i: i + n]
            arr2 = arr[i + n: i + n*2]
            pointer1 = 0
            pointer2 = 0
            counter = i
            while pointer1 < len(arr1) and pointer2 < len(arr2):
                if arr1[pointer1] < arr2[pointer2]:
                    arr[counter] = arr1[pointer1]
                    pointer1 += 1
                else:
                    arr[counter] = arr2[pointer2]
                    pointer2 += 1
                counter += 1

            while pointer1 < len(arr1):
                arr[counter] = arr1[pointer1]
                pointer1 += 1
                counter += 1
            while pointer2 < len(arr2):
                arr[counter] = arr2[pointer2]
                pointer2 += 1
                counter += 1
        n = n*2
        
array = [2, 3, 4, 1, -2, 0, 5, 1]
merge_sort2(array)
print(array)

# >>>

连续子列表的最大和

问题描述

在一个列表中找出连续子列表的最大和，列表中的数字可负可正，并且子列表不能为空

思路解析

1. 列表的最大子列表的和，有三种可能：左子列表，右子列表或左子列表与右子列表之间
2. 左子列表和右子列表答案是知道的，找到左右子列表之间的子列表最大和就可以了
3. 设一个中点，遍历中点左边的值，跟踪记录已遍历过的值的总和，取这些总和的最大值
4. 遍历中点右边的值，同样跟踪记录已遍历过的值的总和，取这些总和的最大值
5. 最后，左面的最大值+右面的最大值+中点值就是第三种可能的答案了

代码实现

def max_sub_array(arr):
    if arr == []:
        return
    if len(arr) == 1:
        return arr[0]
    # 设中点
    cut = len(arr) // 2
    # 分治：找到左子列表最大和
    left_sum = max_sub_array(arr[: cut])
    # 分治：找到右子列表最大和
    right_sum = max_sub_array(arr[cut: ])
    
    left_middle_sum = 0
    max_l = 0
    right_middle_sum = 0
    max_r = 0
    # 找到左子列表与右子列表之间子列表的最大和
    for i in range(cut - 1, -1, -1):
        left_middle_sum += arr[i]
        max_l = max(left_middle_sum, max_l)
    for i in range(cut + 1, len(arr), 1):
        right_middle_sum += arr[i]
        max_r = max(right_middle_sum, max_r)
    # 返回三种可能的最大值
    return (max(left_sum, max_l + arr[cut] + max_r, right_sum))

arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
max_sum = max_sub_array(arr)
print(max_sum)

#>>>

【核心算法9】分治算法

原文：https://www.cnblogs.com/JoshuaP/p/13227485.html