状压DP就是将一个状态压缩为一个整数(通常为二进制数),就可以在更为方便地进行状态转移的同时,达到节约空间的目的。
我们设f[i][j]为当前的状态为\(i\),放置到第\(j\)行时的方案数
但是,因为我们要在\(n \times n\)的棋盘上放置\(n\)个车,所以,我们必定要在每一行都放置一个车
因此,我们可以把第二维省略掉
题目还要求有一些格点不能放车,所以我们要提前把每一行可以放置的位置枚举一下
for(ll i=1;i<=n;i++){
vis[i]=mmax;
}
for(ll i=1;i<=m;i++){
ll aa,bb;
scanf("%lld%lld",&aa,&bb);
vis[aa]-=(1<<(bb-1));
}
下面就是状态转移方程,如果上一行的状态和当前行的状态不冲突
那么当前行的方案数就要加上上一行的方案数
注意要把\(f[0][0]\)初始化为\(0\)
for(ll i=0;i<=mmax;i++){
ll now=solve(i);//枚举当前是第几行
ll can=i&(vis[now]);//枚举当前合法的状态
for(ll j=1;j<=n;j++){
if((can&(1<<(j-1)))==0) continue;//如果当前状态不包括j,直接continue掉
ll las=i^(1<<(j-1)); //枚举上一行状态
f[i]+=f[las];
}
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=23;
ll f[1<<maxn],vis[maxn];
ll n,m;
ll solve(ll xx){
ll ans=0;
for(ll i=1;i<=n;i++){
if(xx&(1<<(i-1))) ans++;
}
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
ll mmax=(1<<n)-1;
for(ll i=1;i<=n;i++){
vis[i]=mmax;
}
for(ll i=1;i<=m;i++){
ll aa,bb;
scanf("%lld%lld",&aa,&bb);
vis[aa]-=(1<<(bb-1));
}
f[0]=1;
for(ll i=0;i<=mmax;i++){
ll now=solve(i);
ll can=i&(vis[now]);
for(ll j=1;j<=n;j++){
if((can&(1<<(j-1)))==0) continue;
ll las=i^(1<<(j-1));
f[i]+=f[las];
}
}
printf("%lld\n",f[mmax]);
return 0;
}
思路和上一道题一样,我们设\(f[i][j][k]\)为当前的行数为\(i\)状态为\(j\)并且放了\(k\)个国王时的方案数
因为第2行的状态要由第1行转移过来,所以我们要提前把第1行的状态处理一下
for(ll i=0;i<=mmax;i++){
if(i&(i<<1) || i&(i>>1)) continue;
f[1][i][solve(i)]=1;
}
在我们转移状态的时候,要注意当前行的状态不能冲突,也不能和上一行的状态冲突
for(ll i=2;i<=n;i++){//枚举行数
for(ll j=0;j<=mmax;j++){//枚举当前行的状态
ll now=solve(j);
if(j&(j<<1) || j&(j>>1)) continue;//当前行的状态不能冲突
for(ll k=0;k<=mmax;k++){//枚举上一行的状态
if(k&j || k&(j<<1) || k&(j>>1)) continue;//上一行的状态不能自己冲突,也不能和当前行的状态冲突
for(ll c=0;c+now<=m;c++){
f[i][j][c+now]+=f[i-1][k][c];
}//枚举放置国王的个数
}
}
}
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=12;
ll f[maxn][1<<maxn][maxn*maxn];
ll n,m;
ll solve(ll xx){
ll ans=0;
for(ll i=1;i<=n;i++){
if(xx&(1<<(i-1))) ans++;
}
return ans;
}
int main(){
scanf("%lld%lld",&n,&m);
ll mmax=(1<<n)-1;
for(ll i=0;i<=mmax;i++){
if(i&(i<<1) || i&(i>>1)) continue;
f[1][i][solve(i)]=1;
}
for(ll i=2;i<=n;i++){
for(ll j=0;j<=mmax;j++){
ll now=solve(j);
if(j&(j<<1) || j&(j>>1)) continue;
for(ll k=0;k<=mmax;k++){
if(k&j || k&(j<<1) || k&(j>>1)) continue;
for(ll c=0;c+now<=m;c++){
f[i][j][c+now]+=f[i-1][k][c];
}
}
}
}
ll ans=0;
for(ll i=1;i<=n;i++){
for(ll j=1;j<=mmax;j++){
ans+=f[i][j][m];
}
}
printf("%lld\n",ans);
return 0;
}

\(m\)的范围很小,所以我们考虑状压\(m\)
因为一个点会影响三行的状态,所以我们定义\(f[i][j][k]\)为当前枚举到第\(i\)行当前行的状态为\(j\)上一行的状态为\(k\)时的方案数
其他的和上一题一模一样
因为这一道题卡空间和时间,所以我们需要把合法的状态预处理出来
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=11;
typedef long long ll;
ll f[maxn*10][65][65],a[maxn*10],mmax;
char c[maxn*10][maxn];
ll zt[65],num[65];
ll n,m;
ll solve(ll xx){
ll ans=0;
for(ll i=0;i<m;i++){
if(xx&(1<<i)) ans++;
}
return ans;
}
ll cnt=0;
void chuli(){
for(ll i=0;i<mmax;i++){
if(i&(i<<1) || i&(i<<2)) continue;
cnt++;
zt[cnt]=i;
num[cnt]=solve(i);
}
}
int main(){
scanf("%lld%lld",&n,&m);
for(ll i=1;i<=n;i++){
scanf("%s",c[i]+1);
}
mmax=1<<m;
for(ll i=1;i<=n;i++){
for(ll j=1;j<=m;j++){
if(c[i][j]==‘P‘){
a[i]+=(1<<(j-1));
}
}
}
chuli();
ll ans=-1;
for(ll i=1;i<=n;i++){
for(ll j=1;j<=cnt;j++){
if(zt[j]!=(zt[j]&a[i])) continue;
if(i==1){
f[1][j][0]=max(f[i][j][0],num[j]);
ans=max(ans,f[1][j][0]);
}
else if(i==2){
for(ll k=1;k<=cnt;k++){
if(zt[k]!=(zt[k]&a[1])) continue;
if(zt[j]&zt[k]) continue;
f[2][j][k]=max(f[2][j][k],f[1][k][0]+num[j]);
ans=max(ans,f[2][j][k]);
}
} else {
for(ll k=1;k<=cnt;k++){
if(zt[k]!=(zt[k]&a[i-1])) continue;
if(zt[k]&zt[j]) continue;
for(ll l=1;l<=cnt;l++){
if(zt[l]!=(zt[l]&a[i-2])) continue;
if(zt[l]&zt[j] || zt[l]&zt[k]) continue;
f[i][j][k]=max(f[i][j][k],f[i-1][k][l]+num[j]);
ans=max(ans,f[i][j][k]);
}
}
}
}
}
printf("%lld\n",ans);
return 0;
}
Farmer John has purchased a lush new rectangular pasture composed of M by N (1 ≤ M ≤ 12; 1 ≤ N ≤ 12) square parcels. He wants to grow some yummy corn for the cows on a number of squares. Regrettably, some of the squares are infertile and can‘t be planted. Canny FJ knows that the cows dislike eating close to each other, so when choosing which squares to plant, he avoids choosing squares that are adjacent; no two chosen squares share an edge. He has not yet made the final choice as to which squares to plant.
Being a very open-minded man, Farmer John wants to consider all possible options for how to choose the squares for planting. He is so open-minded that he considers choosing no squares as a valid option! Please help Farmer John determine the number of ways he can choose the squares to plant.
农场主John新买了一块长方形的新牧场,这块牧场被划分成M行N列(1 ≤ M ≤ 12; 1 ≤ N ≤ 12),每一格都是一块正方形的土地。John打算在牧场上的某几格里种上美味的草,供他的奶牛们享用。
遗憾的是,有些土地相当贫瘠,不能用来种草。并且,奶牛们喜欢独占一块草地的感觉,于是John不会选择两块相邻的土地,也就是说,没有哪两块草地有公共边。
John想知道,如果不考虑草地的总块数,那么,一共有多少种种植方案可供他选择?(当然,把新牧场完全荒废也是一种方案)
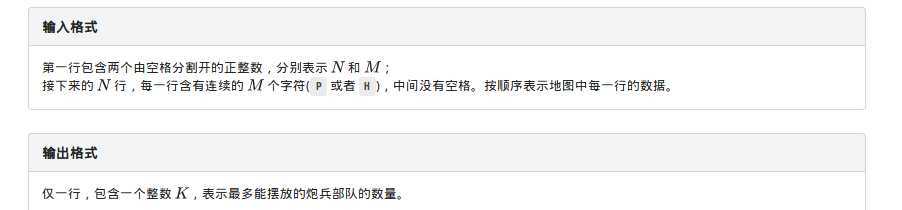
第一行:两个整数M和N,用空格隔开。
第2到第M+1行:每行包含N个用空格隔开的整数,描述了每块土地的状态。第i+1行描述了第i行的土地,所有整数均为0或1,是1的话,表示这块土地足够肥沃,0则表示这块土地不适合种草。
输出格式
一个整数,即牧场分配总方案数除以100,000,000的余数。
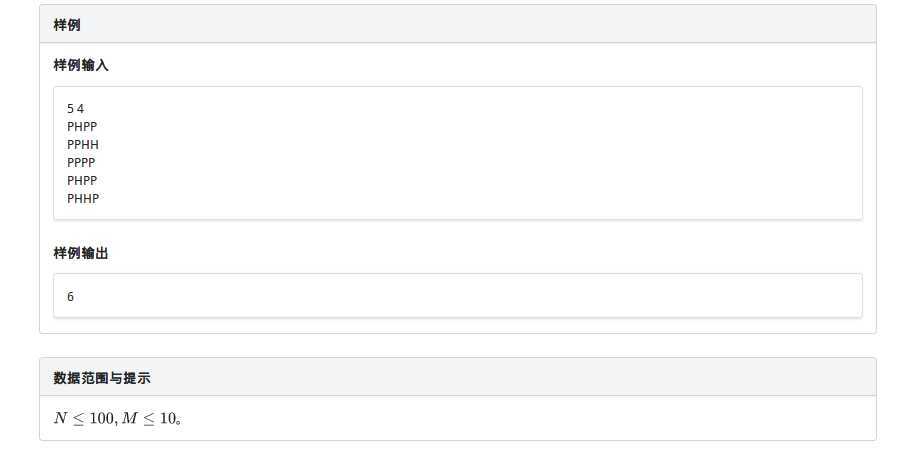
输入 #1
2 3
1 1 1
0 1 0
输出 #1
9
一样的套路,一样的方程定义,一样的状态转移
#include<bits/stdc++.h>
using namespace std;
const int maxn=15;
typedef long long ll;
ll f[maxn][1<<maxn],zt[maxn];
int main(){
int m,n;
scanf("%d%d",&m,&n);
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
int aa;
scanf("%d",&aa);
if(aa==1) zt[i]+=(1<<(j-1));
}
}
int mmax=(1<<n)-1;
f[1][0]=1;
for(int i=0;i<=mmax;i++){
if((i&zt[1])!=i || i&(i<<1) || i&(i>>1)) continue;
f[1][i]=1;
}
for(int i=2;i<=m;i++){
for(int j=0;j<=mmax;j++){
if((j&zt[i])!=j) continue;
if(j&(j<<1) || j&(j>>1)) continue;
for(int k=0;k<=mmax;k++){
if((k&zt[i-1])!=k) continue;
if(k&j || k&(k<<1) || k&(k>>1)) continue;
f[i][j]+=f[i-1][k];
}
}
}
ll ans=0;
for(int i=0;i<=mmax;i++){
ans+=f[m][i];
ans%=100000000;
}
printf("%lld\n",ans);
return 0;
}
Each of Farmer John‘s N (4 <= N <= 16) cows has a unique serial number S_i (1 <= S_i <= 25,000). The cows are so proud of it that each one now wears her number in a gangsta manner engraved in large letters on a gold plate hung around her ample bovine neck.
Gangsta cows are rebellious and line up to be milked in an order called ‘Mixed Up‘. A cow order is ‘Mixed Up‘ if the sequence of serial numbers formed by their milking line is such that the serial numbers of every pair of consecutive cows in line differs by more than K (1 <= K <= 3400). For example, if N = 6 and K = 1 then 1, 3, 5, 2, 6, 4 is a ‘Mixed Up‘ lineup but 1, 3, 6, 5, 2, 4 is not (since the consecutive numbers 5 and 6 differ by 1).
How many different ways can N cows be Mixed Up?
For your first 10 submissions, you will be provided with the results of running your program on a part of the actual test data.
POINTS: 200
约翰家有N头奶牛,第i头奶牛的编号是Si,每头奶牛的编号都是唯一的。这些奶牛最近 在闹脾气,为表达不满的情绪,她们在挤奶的时候一定要排成混乱的队伍。在一只混乱的队 伍中,相邻奶牛的编号之差均超过K。比如当K = 1时,1, 3, 5, 2, 6, 4就是一支混乱的队伍, 而1, 3, 6, 5, 2, 4不是,因为6和5只差1。请数一数,有多少种队形是混乱的呢?
Line 1: Two space-separated integers: N and K
Lines 2..N+1: Line i+1 contains a single integer that is the serial number of cow i: S_i
输入 #1
4 1
3
4
2
1
输出 #1
2
说明/提示
The 2 possible Mixed Up arrangements are:
3 1 4 2
2 4 1 3
\(n\)的值达到了\(16\),如果我们去枚举全排列的话,必定会超时
所以这就要用到一种新的定义方式\(f[i][j]\)为状态为\(i\)的人已经排好了队,队尾的人为\(j\)时合法的方案数
原文:https://www.cnblogs.com/liuchanglc/p/13231580.html