


3 3 1 2 2 1 2 3
1

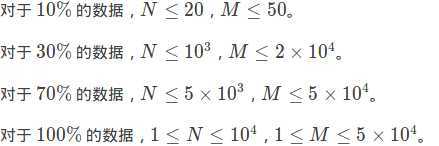
这道题明显的是tarjan,但是只知道tarjan是解不了的,我们分析可以的到最受欢迎的牛只可能是强联通分量中的出度为零的点,只有一个,假如有两个出度为零的点,那么就会形成两个SCC,进而没有牛会受到所有的奶牛的喜欢,进而就不会存在明星奶牛,所以我们统计所有点的出度,如果出度大于1,直接输出0,结束就可以了,然后再找那一个出度为0的点,输出他的sum值就行,sum存这一个SCC中的点数量。
#include<bits/stdc++.h> using namespace std; const int N=5e4+10; int n,m,x,y; int sta[N],head[N],dfn[N],low[N]; int top,tot,Time,cnt,g[N],sum[N]; bool vis[N]; int cd[N]; struct edge{ int to; int ne; }e[N]; void add(int u,int v){ e[++cnt].to = v; e[cnt].ne = head[u]; head[u] = cnt; } void tarjan(int u){//缩点板子基操 dfn[u]=low[u]=++Time; vis[u]=1;sta[++top]=u; for(int i=head[u];i;i=e[i].ne){ int v = e[i].to; if(!dfn[v]){ tarjan(v); low[u] = min( low[u] , low[v]); } if(vis[v]){ low[u] = min(low[u] , dfn[v]); } } if(dfn[u] == low[u]){ tot++; while(sta[top+1]!=u){ int v = sta[top--]; vis[v] = 0; g[v] = tot; sum[tot]++; } } } int main(){ scanf("%d%d",&n,&m); for(int i=1;i<=m;i++){ scanf("%d%d",&x,&y); add(x,y); } for(int i=1;i<=n;i++){ if(!dfn[i])tarjan(i); } for(int i=1;i<=n;i++){ for(int j=head[i];j;j=e[j].ne){ int v = e[j].to; if(g[i]!=g[v]){ cd[g[i]]++; } } } int pos=0; for(int i=1;i<=tot;i++){ if(!cd[i]){ if(pos){//如果有第二个出度为零的点就结束 printf("0\n"); return 0; } pos=i; } } printf("%d\n",sum[pos]); return 0; }
点关注不迷路,点推荐不妄心
P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G
原文:https://www.cnblogs.com/LightyaChoo/p/13231653.html