Sierpinski三角形是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。其生成过程为:
(1)取一个三角形(多数使用等边三角形);
(2)沿三边中点连线,将它分成四个小三角形;
(3)对上、左、右这三个小三角形重复这一过程。
SierPinski三角形的生成示意如图1所示。
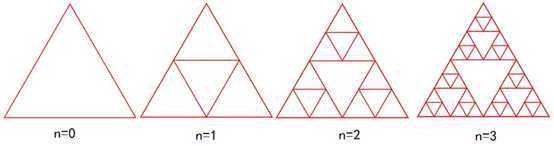
图1 SierPinski三角形的生成
SierPinski三角形采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>SierPinski三角形</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById(‘myCanvas‘);
var ctx = canvas.getContext(‘2d‘);
var depth =5;
ctx.strokeStyle = "red";
ctx.lineWidth = 3;
function sierpinski(x1,y1,x2,y2,x3,y3,n)
{
if (n<0) return;
ctx.beginPath();
ctx.moveTo(x1,y1);
ctx.lineTo(x2,y2);
ctx.lineTo(x3,y3);
ctx.lineTo(x1,y1);
ctx.closePath();
ctx.stroke();
var x4 = (x1 + x2) / 2;
var y4 = (y1 + y2) / 2;
var x5 = (x2 + x3) / 2;
var y5 = (y2 + y3) / 2;
var x6 = (x1 + x3) / 2;
var y6 = (y1 + y3) / 2;
sierpinski(x1,y1,x4,y4,x6,y6,n-1);
sierpinski(x6,y6,x5,y5,x3,y3,n-1);
sierpinski(x4,y4,x2,y2,x5,y5,n-1);
}
sierpinski(300, 500-500*Math.sqrt(3)/2, 50, 500, 550, 500,depth);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的SierPinski三角形,如图2所示。

图2 递归深度depth =5的SierPinski三角形
SierPinski垫片的生成过程为:
(1)取一个实心的三角形(多数使用等边三角形);
(2)沿三边中点连线,将它分成四个小三角形,
(3)去掉中间的那一个小三角形;
(4)对其余三个小三角形重复这一过程。
SierPinski垫片的生成示意如图3所示。
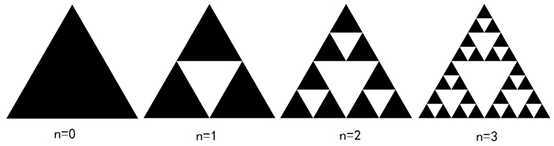
图3 SierPinski垫片的生成
SierPinski垫片采用递归过程易于实现,编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>SierPinski垫片</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById(‘myCanvas‘);
var ctx = canvas.getContext(‘2d‘);
ctx.beginPath();
ctx.moveTo(300, 500-500*Math.sqrt(3)/2);
ctx.lineTo(50,500);
ctx.lineTo(550,500);
ctx.closePath();
ctx.fillStyle="black";
ctx.fill();
var depth =5;
ctx.fillStyle = "white";
function sierpinski(x1,y1,x2,y2,x3,y3,n)
{
if (n<=0) return;
var x4 = (x1 + x2) / 2;
var y4 = (y1 + y2) / 2;
var x5 = (x2 + x3) / 2;
var y5 = (y2 + y3) / 2;
var x6 = (x1 + x3) / 2;
var y6 = (y1 + y3) / 2;
ctx.beginPath();
ctx.moveTo(x4,y4);
ctx.lineTo(x5,y5);
ctx.lineTo(x6,y6);
ctx.closePath();
ctx.fill();
sierpinski(x1,y1,x4,y4,x6,y6,n-1);
sierpinski(x6,y6,x5,y5,x3,y3,n-1);
sierpinski(x4,y4,x2,y2,x5,y5,n-1);
}
sierpinski(300, 500-500*Math.sqrt(3)/2, 50, 500, 550, 500,depth);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出的SierPinski垫片,如图4所示。

图4 递归深度depth =5的SierPinski垫片
SierPinski垫片的初始图形是三角形,如果将初始图形改成正方形,便可以得到称为SierPinski地毯的图形。它的生成过程为:
(1)取一个实心的正方形;
(2)将正方形的每边三等分,并连接相应的等分点,从而将原正方形等分为面积相等的9个小正方形;
(3)去掉中间的那一个小正方形;
(4)对其余的8个小正方形重复这一过程。
SierPinski垫片的生成示意如图5所示。
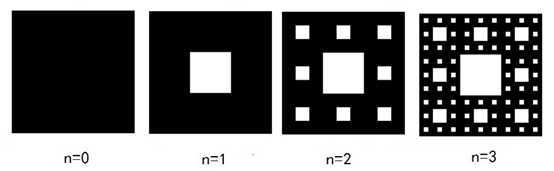
图5 SierPinski地毯的生成
设正方形的左上角坐标为(x,y),边长为L,则中间正方形的左上角坐标和边长分别为(x+L/3,y+L/3)和L/3,其余8个小正方形的边长均为L/3,左上角坐标分别为(x,y)、(x+L/3,y)、(x+2*L/3,y)、(x,y+L/3)、(x+2*L/3,y+L/3)、(x,y+2*L/3)、(x+L/3,y+2*L/3)和(x+2*L/3,y+2*L/3)。
为了绘制SierPinski地毯,可以编写如下的HTML代码。
<!DOCTYPE html>
<head>
<title>SierPinski地毯</title>
</head>
<body>
<canvas id="myCanvas" width="600" height="600" style="border:3px double #996633;">
</canvas>
<script type="text/javascript">
var canvas = document.getElementById(‘myCanvas‘);
var ctx = canvas.getContext(‘2d‘);
ctx.fillStyle="black";
ctx.fillRect(50,50,450,450);
var depth =5;
ctx.fillStyle = "white";
function sierpinski(x,y,L,n)
{
if (n<=0) return;
ctx.fillRect(x+L/3,y+L/3,L/3,L/3);
sierpinski(x,y,L/3,n-1);
sierpinski(x+L/3,y,L/3,n-1);
sierpinski(x+2*L/3,y,L/3,n-1);
sierpinski(x,y+L/3,L/3,n-1);
sierpinski(x+2*L/3,y+L/3,L/3,n-1);
sierpinski(x,y+2*L/3,L/3,n-1);
sierpinski(x+L/3,y+2*L/3,L/3,n-1);
sierpinski(x+2*L/3,y+2*L/3,L/3,n-1);
}
sierpinski(50,50,450,depth);
</script>
</body>
</html>
在浏览器中打开包含这段HTML代码的html文件,可以看到在浏览器窗口中绘制出SierPinski垫片,如图6所示。

图6 递归深度depth =5的SierPinski地毯
原文:https://www.cnblogs.com/cs-whut/p/13233655.html