概率图：高斯混合模型（GMM）

高斯混合模型（Gaussian Mixture model）

                                                                    来源：B站up主：shuhuai008，板书

问题：“高斯”？，“混合”？

可从两个角度理解

一、从几何角度看：高斯混合模型就是若干个高斯模型的“加权平均”。【个人理解：“混合”体现在高斯分布的叠加，也体现在“隐变量”和观测变量的引入】

公式目的其实就是求解xi的概率密度函数；

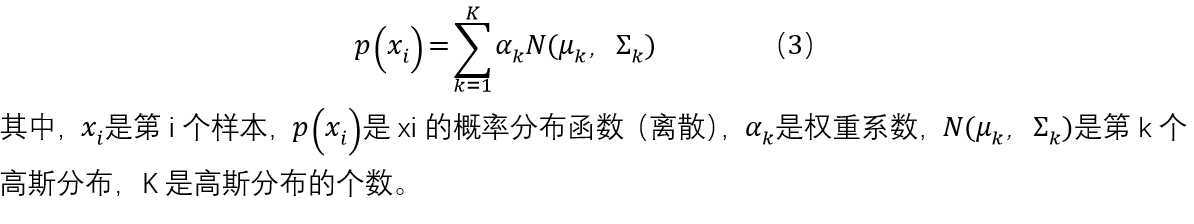
                                        混合高斯分布的公式

二、从“生成”/“混合”的角度看

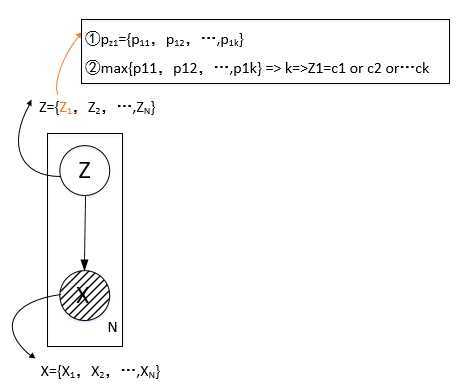
      GMM模型的概率图表示，及相关概念示意图

Z是“隐变量”，X是观测变量，由隐变量生成观测变量的过程就是混合高斯模型的生成过程。X在概率图中用阴影表示可观测。N表示有N个样本{x1,x2...xN}，对应的也就有N个隐变量{Z1,Z2,...ZN}。Z1表示第一个样本的隐变量，Z1是一个离散的随机变量，Z1的概率密度函数如板书所示。p_z1(c1)=p₁₁，p_z1(c2)=p₁₂,...p_z1(ck)=p_1k；所以将p_z1简略表示成p_z1={p₁₁,p₁₂,...p_1k}个，找出pz1中最大的概率，假如max{p₁₁,p₁₂,...p_1k}=p₁₄，那么z1属于第4个高斯分布的概率最大，所以将Z1归入第四个高斯分布。其实Z1就相当于一个指示变量，Z1=c4表明Z1属于第四个高斯分布的概率最大。其中c1,c2,...ck分别是各个高斯分布的中心点（c1..ck和x1,...xN的向量维度相同，此处可类比聚类算法中的聚类中心）。

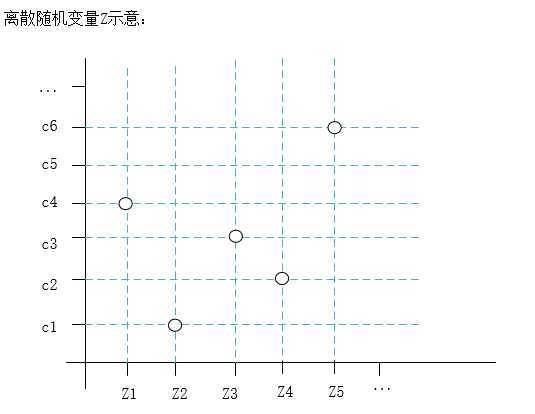
 “离散”指的是z1的值域是离散的数值{c1,c2...ck}，只能从这几个中选。

“随机”指的是z1取c1，c2,...ck等数值的概率是确定的，但是在某一个样本的观测中具体取哪个值是随机的。【个人理解】

概率图：高斯混合模型（GMM）

原文：https://www.cnblogs.com/feynmania/p/13254222.html