再探快速傅里叶变换(FFT)(其四) 多项式操作

省选前夕爆补一波多项式全家桶,存一些板子

多项式乘法

不解释。注意如果式子太复杂，直接全部DFT再按原式子算,最后IDFT。封装后不一定好用

void mul(ll *a,ll *b,ll  *c,ll n,ll m){
    static ll ta[maxn+5],tb[maxn+5];
    int N=1,L=0;
    while(N<=n+m) N*=2,L++;
    for(int i=0;i<N;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    for(int i=0;i<N;i++) ta[i]=(i<n?a[i]:0);
    for(int i=0;i<N;i++) tb[i]=(i<m?b[i]:0);
    NTT(ta,N,1);
    NTT(tb,N,1);
    for(int i=0;i<N;i++) c[i]=ta[i]*tb[i]%mod;
    NTT(c,N,-1);
}

多项式求逆

定义:给出\(n-1\)次多项式\(f(x)\),我们要求一个多项式\(g(x)\),满足\(f(x)g(x) \equiv 1(\bmod \ x^n)\).
系数对NTT模数取模.

求逆的算法基于倍增,是迭代进行的。假设我们已经求出了一个\(h(x)\),满足\(f(x)h(x) \equiv 1 (\bmod\ x^{\frac{n}{2}})\)

由定义有\(f(x)g(x) \equiv 1(\bmod\ x^{\frac{n}{2}})\)

两式做差,的\(h(x)-g(x) \equiv 1 (\bmod x^{\frac{n}{2}})\)

平方,得\(h^2(x)-2h(x)g(x)+g^2(x) \equiv 1(\bmod\ x^n)\)

两边同时乘上\(f(x)\),将\(f(x)g(x)=1\)代入,移项可得:

因此递归求出\(h(x)\)后,就可以推出\(g(x)\).边界条件\(n=1\)时\(g_0=f_0^{-1}\). 时间复杂度满足递推式\(T(n)=T(\frac{n}{2})+n \log n\),根据主定理为\(\Theta(n\log n)\)

void get_inv(ll *f,ll *g,int n){
    static ll fp[maxn+5];
    if(n==1){
        g[0]=inv(f[0]);
        return;
    }
    get_inv(f,g,(n+1)/2);
    int N=1,L=0;
    while(N<n*2) N*=2,L++;
    for(int i=0;i<N;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    for(int i=0;i<N;i++){
        if(i<n) fp[i]=f[i];
        else fp[i]=0;
    }
    NTT(fp,N,1);
    NTT(g,N,1);
    for(int i=0;i<N;i++) g[i]=g[i]*(2-fp[i]*g[i]%mod+mod)%mod;
    NTT(g,N,-1);
    for(int i=n;i<N;i++) g[i]=0;
}

多项式取余

定义:[LuoguP4512]给定一个\(n\)次多项式\(f(x)\)和一个\(m\)次多项式\(g(x)\),求两个多项式\(q(x),r(x)\).满足\(f(x)=q(x)g(x)+r(x)\),且\(q(x)\)次数为\(n-m\),\(r(x)\)次数小于\(m\).模数为NTT模数。

我们先定义一种操作\(r\),若\(f(x)=\sum_{i=0}^{n}a_ix^i\),则\(f_r(x)=\sum_{i=0}^{n-1}a_ix^{n-i}\).实际上就是把系数顺序倒过来。容易发现\(f_r(x)=x^nf(\frac{1}{x})\).接下来开始推式子

我们只需要在\(\bmod\ x^{n-m+1}\)下对\(g_r\)求逆,就能求出\(q_r\)和\(q\),然后用\(r(x)=f(x)-g(x)q(x)\)求出\(r\).

//a就是f,b就是g
void div_mod(ll *a,ll *b,ll *q,ll *r,int n,int m){
    static ll ra[maxn+5],rb[maxn+5],invrb[maxn+5];
    for(int i=0;i<n;i++) ra[i]=a[i];
    for(int i=0;i<m;i++) rb[i]=b[i];
    reverse(ra,ra+n);
    reverse(rb,rb+m);
    for(int i=n-m+1;i<n*2;i++) rb[i]=0;
    get_inv(rb,invrb,n-m+1); //在mod x^(n-m+1)下做 
    mul(ra,invrb,q,n,n-m+1);
    for(int i=n-m+1;i<n*2;i++) q[i]=0;
    reverse(q,q+n-m+1);
    mul(q,b,r,n-m+1,m);
    for(int i=0;i<n;i++) r[i]=(a[i]-r[i]+mod)%mod;
}

多项式ln

定义:给出\(n-1\)次多项式\(f(x)\),我们要求一个多项式\(g(x)\),满足\(g(x) \equiv \ln f(x)(\bmod \ x^n)\).
系数对NTT模数取模

对上式求导,\(g‘(x)=[\ln f(x)]‘=\ln‘(f(x))\cdot f‘(x)=\frac{f‘(x)}{f(x)}\)

这样就可以用多项式求逆得到\(g‘(x)\),再积分回去就好了。

void get_deriv(ll *a,int n){//求导 
    for(int i=1;i<=n;i++) a[i-1]=a[i]*i%mod;//(x^a)‘=ax^(a-1)
    a[n]=0;
}
void get_inter(ll *a,int n){//积分 
    for(int i=n;i>=1;i--) a[i]=a[i-1]*inv(i)%mod;
    a[0]=0;
}
void get_ln(ll *a,ll *b,int n){
    static ll A[maxn+5],B[maxn+5];
    memset(A,0,sizeof(A));
    memset(B,0,sizeof(B));
    for(int i=0;i<n;i++) A[i]=a[i];
    get_deriv(A,n);
    get_inv(a,B,n);
    int N=1,L=0;
    while(N<=n*2) N*=2,L++;
    for(int i=0;i<N;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(A,N,1);
    NTT(B,N,1);
    for(int i=0;i<N;i++) b[i]=A[i]*B[i]%mod;
    NTT(b,N,-1);
    get_inter(b,N);
    for(int i=n;i<N;i++) b[i]=0; 
}

多项式exp

牛顿迭代

牛顿迭代是一种求方程近似解的方法。

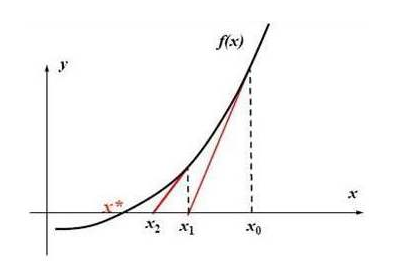
如图,先选取一个初始值\(x_0\),向上做垂线与\(f(x)\)的图像相交。作\(f(x)\)在\(x_0\)处的切线交\(x\)轴于\(x_1\),从\(x_1\)再向上做垂线,如此迭代,\(x_i\)会逐渐趋近于方程的解。

我们来推导迭代的表达式。由导数的几何意义,\(x_i\)处切线方程为\(y=f‘(x_i)x+f(x_i)-f‘(x_i)x_i\).令\(y=0\),得交点坐标\(x_{i+1}=x_{i}-\frac{f(x_i)}{f‘(x_i)}\)

其中迭代的实数\(x_i\)也可以换成一个多项式。

exp的求解

定义:给出\(n-1\)次多项式\(f(x)\),我们要求一个多项式\(g(x)\),满足\(g(x) \equiv \mathrm{e}^{f(x)} (\bmod\ x^n)\).
系数对NTT模数取模

对上式两边求\(\ln\),得\(\ln(g(x))-f(x) \equiv 0(\bmod\ x^n)\)

令\(B(t(x))=\ln(t(x))-f(x)\),把\(t(x)\)看成自变量,用牛顿迭代求使得\(B(t(x))=0\)的\(t(x)\)

我们设第\(i\)次迭代后的根为\(g_i(x)\),根据牛顿迭代的公式有:

注意\(H‘(g_{i}(x))=\frac{1}{g_{i}(x)}\),因为我们把\(g_{i}(x)\)看作自变量,\(f(x)\)看作常数。

每次迭代都使得精度翻倍(指的是最高次翻倍,即\(g_{i}(x)\)满足\(\ln(g(x))-f(x) \equiv 0(\bmod\ x^{2^i})\)).复杂度\(T(n)=T(\frac{n}{2})+n\log_2n\),即\(\Theta(n\log n)\)

void get_exp(ll *a,ll *b,int n){
    static ll lnb[maxn+5];
    if(n==1){
        b[0]=1;
        return;
    }
    get_exp(a,b,(n+1)/2);
    get_ln(b,lnb,n);
    int N=1,L=0;
    while(N<=n*2) N*=2,L++;
    for(int i=0;i<N;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    for(int i=0;i<n;i++) lnb[i]=(a[i]-lnb[i]+mod)%mod;
    for(int i=n;i<N;i++) lnb[i]=0;
    lnb[0]++;
    NTT(lnb,N,1);
    NTT(b,N,1);
    for(int i=0;i<N;i++) b[i]=b[i]*lnb[i]%mod;
    NTT(b,N,-1);
    for(int i=n;i<N;i++) b[i]=0; 
} 

多项式快速幂

多项式快速插值

再探快速傅里叶变换(FFT)(其四) 多项式操作

原文：https://www.cnblogs.com/birchtree/p/13263252.html