数电（2）：逻辑代数的基本定理

一、概述

• 逻辑：是指事物间的因果关系
• 二值逻辑：是指两种对立逻辑状态的逻辑关系。
• 逻辑代数：1849年英国数学家乔治，布尔( George Boole)首先提出了进行逻辑运算的数学方法————布尔代数。后来，由于布尔代数被广泛应用于解决开关电路和数字逻辑电路的分析与设计中，所以也将布尔代数称为开关代数或逻辑代数。逻辑代数就是布尔代数在二值逻辑电路中的应用。
• 逻辑变量：逻辑代数中的变量，常用字母表示。

二、逻辑代数中的基本运算

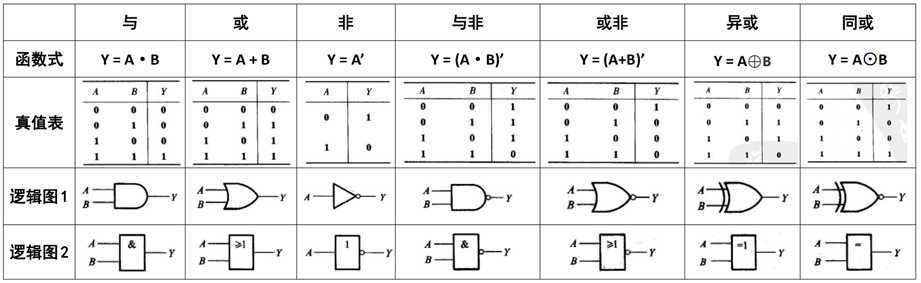
三、基本公式和常用公式

1、基本公式

（1）运算规则

0·A = 0    1·A = A
0+A = A    1+A = A

（2）重叠律

A·A = A
A+A = A

（3）互补律

A·A‘ = 0
A+A‘ = 1

（4）分配律

A·B = B·A
A+B = B+A

（5）反演律（摩根定理）

(A·B)‘ = A‘+B‘
(A+B)‘ = A‘·B‘

（6）还原律

(A‘)‘ = A

2、常用公式

--------------------------
A+A·B = A
--------------------------
A+A‘·B = A+B
--------------------------
A·B+A·B‘ = A
--------------------------
A·(A+B) = A
--------------------------
A·B+A‘·C+B·C = A·B+A‘·C
A·B+A‘·C+BCD = A·B+A‘·C
--------------------------
A·(A·B)‘  = A·B‘
A‘·(A·B)‘ = A‘
--------------------------

ps：· 可以省略，即 A·B 可以写作 AB。

四、基本定理

1、代入定理：在任何一个包含变量A的逻辑等式中，若以另外一个逻辑式代入式中所有A的位置，则等式仍然成立。

2、对偶定理：两逻辑式相等，则其对偶式也相等。

• 对偶式Y^D： · 和 + 互换，0 和 1 互换

3、反演定理：逻辑式 Y，其对偶式结果为 Y‘。

• ①先括号、然后乘、最后加。
• ②非单变量的反号应保留不变。

五、逻辑函数及其表示方法

1、逻辑函数

　　以逻辑变量作为输入，以运算结果作为输出，二者之间是一种函数关系，写作：Y = F（A，B，C，...）。

2、表示方法

（1）逻辑真值表

（2）逻辑函数式

（3）逻辑图

（4）波形图

　　如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列起来,就得到了表示该逻辑函数的波形图。这种波形图(waveform)也称为时序图( timing diagram)。

例如：Y = A（B+C）

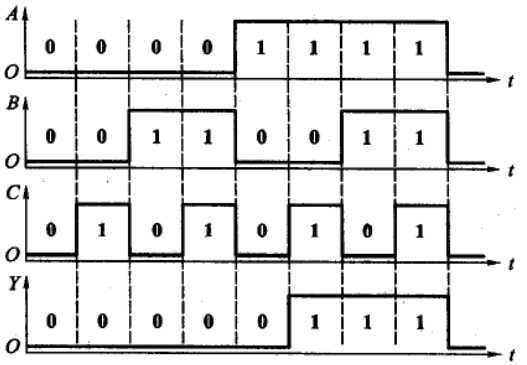
 3、表示方法互化

（1）真值表化函数式

• ①找出真值表中使逻辑函数 Y=1 的那些输人变量取值的组合。
• ②每组输人变量取值的组合对应一个乘积项，其中取值为1的写人原变量，取值为 0 的写人反变量。
• ③将这些乘积项相加，即得 Y 的逻辑函数式。

（2）函数式化真值表

　　代数字进去对应列表即可。

（3）函数式化逻辑图

　　逻辑图像符号代替逻辑函数式中的逻辑运算符号，并按优先顺序连接起来即可。

（4）逻辑图化函数式

　　从逻辑图的输入端到输出端，逐级写到每个图像符号的输出逻辑式即可。

（5）波形图化真值表

　　从波形图上找到每个时间段里输入变量与函数输出的取值，对应列表即可。

（6）真值表化波形图

　　将真值表中所有的输入变量与对应的输出变量的取值，一次排列画成以时间为横轴的波形即可。

4、逻辑函数的两种标准形式

略

5、逻辑函数形式的变换

略

六、逻辑函数的化简方法

1、公式化简法

• 并项法
• 吸收法
• 消项法
• 消因子法
• 配项法

2、卡诺图化简法

（1）表示方法

（2）化简过程

3、奎恩-麦克拉斯基化简法（Q-M法）

　　过程比较繁琐，很少有人手工用此法化简复杂的逻辑函数，但流程确定，因此可以使用其原理编制软件，在计算机上完成化简工作。

略

参考资料：阎石. 数字电子技术基础(第5版)[M]. 高等教育出版社, 2006.

数电（2）：逻辑代数的基本定理

原文：https://www.cnblogs.com/xianyufpga/p/13263600.html