求两数之和（leedcode）

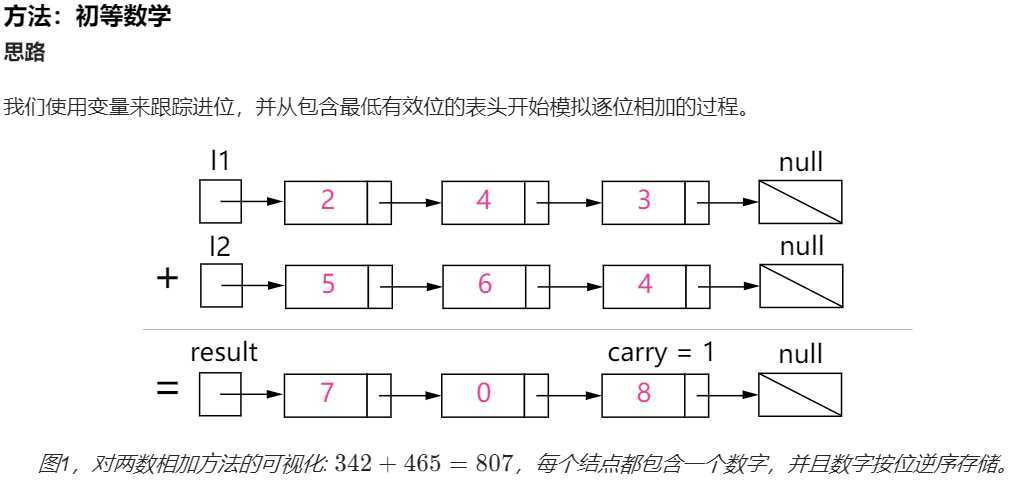
算法

就像你在纸上计算两个数字的和那样，我们首先从最低有效位也就是列表 l1l1 和 l2l2 的表头开始相加。由于每位数字都应当处于 0 \ldots 90…9 的范围内，我们计算两个数字的和时可能会出现 “溢出”。例如，5 + 7 = 125+7=12。在这种情况下，我们会将当前位的数值设置为 22，并将进位 carry = 1carry=1 带入下一次迭代。进位 carrycarry 必定是 00 或 11，这是因为两个数字相加（考虑到进位）可能出现的最大和为 9 + 9 + 1 = 199+9+1=19。

伪代码如下：

将当前结点初始化为返回列表的哑结点。
将进位 carrycarry 初始化为 00。
将 pp 和 qq 分别初始化为列表 l1l1 和 l2l2 的头部。
遍历列表 l1l1 和 l2l2 直至到达它们的尾端。
将 xx 设为结点 pp 的值。如果 pp 已经到达 l1l1 的末尾，则将其值设置为 00。
将 yy 设为结点 qq 的值。如果 qq 已经到达 l2l2 的末尾，则将其值设置为 00。
设定 sum = x + y + carrysum=x+y+carry。
更新进位的值，carry = sum / 10carry=sum/10。
创建一个数值为 (sum \bmod 10)(summod10) 的新结点，并将其设置为当前结点的下一个结点，然后将当前结点前进到下一个结点。
同时，将 pp 和 qq 前进到下一个结点。
检查 carry = 1carry=1 是否成立，如果成立，则向返回列表追加一个含有数字 11 的新结点。
返回哑结点的下一个结点。
请注意，我们使用哑结点来简化代码。如果没有哑结点，则必须编写额外的条件语句来初始化表头的值。

转载的链接：https://leetcode-cn.com/problems/add-two-numbers/solution/liang-shu-xiang-jia-by-leetcode/

class Solution {
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
        ListNode dummyHead=new ListNode(0);
        ListNode p=l1,q=l2,curr=dummyHead;
        int carry=0;
        while(p!=null || q!=null){
            int x=(p!=null)?p.val:0;
            int y=(q!=null)?q.val:0;
            int sum=x+y+carry;
            carry=sum/10;
            curr.next = new ListNode(sum % 10);
            curr = curr.next;
            if(p!=null) p=p.next;
            if(q!=null) q=q.next;
        }
        if(carry>0){
            curr.next=new ListNode(1);
        }
       return dummyHead.next;

    }
     
}

求两数之和（leedcode）

原文：https://www.cnblogs.com/wanshiliang/p/13263707.html