两组数据只是建边顺序换了,图是一样的
最后输出
(i,low[i],dfn[i])
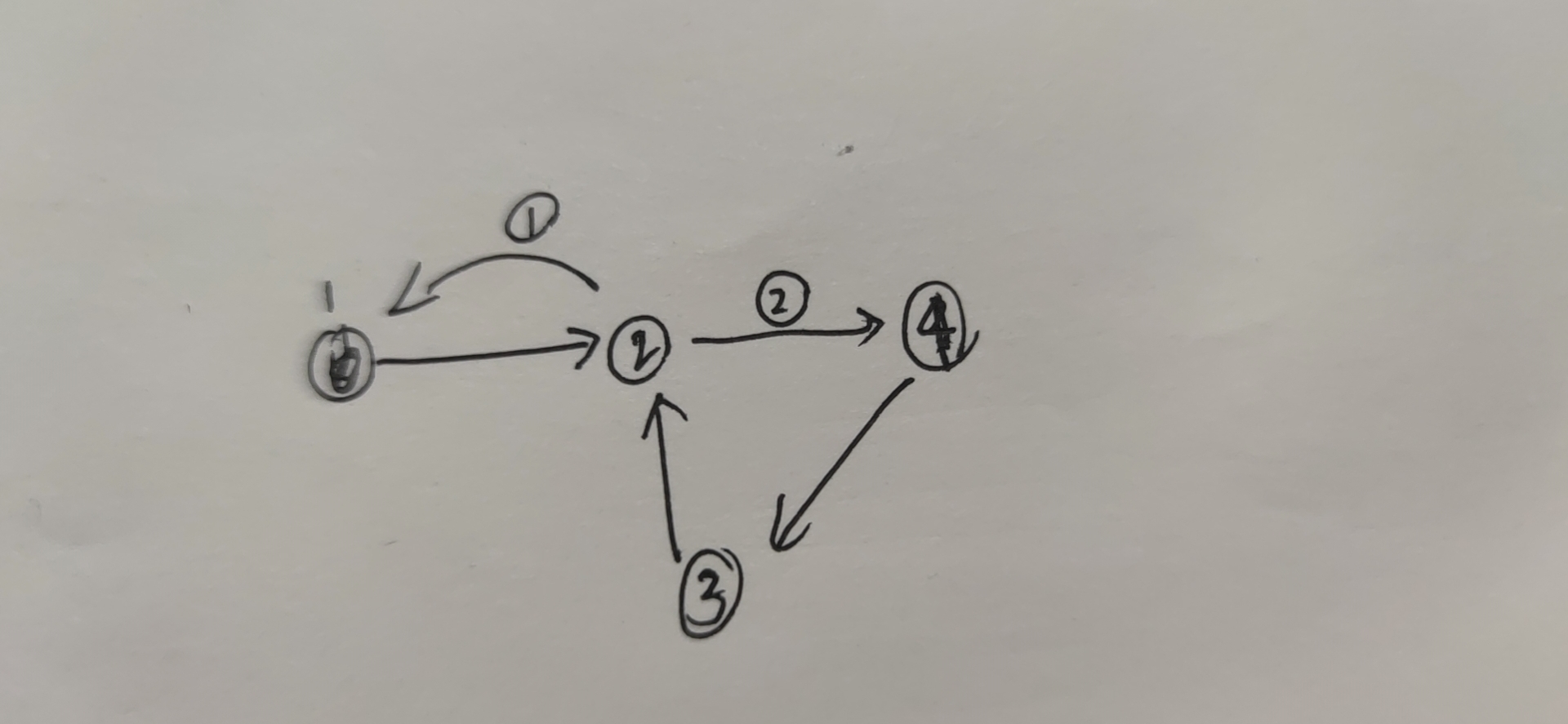
第一种:先走路1,再走路2,也就是先走了回头路,访问到了栈中之前的点,再递归没有访问过的点
4 5
1 2
2 1
2 4
4 3
3 2
用low更新
1:1 1
2:1 2
3:1 4
4:1 3
用dfn更新
1:1 1
2:1 2
3:2 4
4:2 3
第二种:先走路2,再走路1
4 5
1 2
2 4
2 1
4 3
3 2
用low更新
1:1 1
2:1 2
3:2 4
4:2 3
用dfn更新
1:1 1
2:1 2
3:2 4
4:2 3
总结:用low还是用dfn,都不会影响最终求出来的强连通分量的结果。在求强连通分量的时候必须要满足递归完所有相邻点后仍然有\(low[u]==dfn[u]\),考察这些可能成为根的点。上述两种建图方式,如果先走了回头路,无论哪种更新方式,low[2]不超过1,所以点2不可能是强连通分量的根,后续递归中,无论用dfn/low更新,4,3都不可能是强连通分量的根;如果后走回头路,虽然从2开始的递归会让后面所有的low都等于2,但是递归回2以后,2的相邻边还没有走完,还不能判断low==dfn这个条件,所以会用1号点的信息更新low[2],但无论是low[1]/dfn[1]来更新,都不会使点2成为那个\(low==dfn\)的点。
【图论】【探究】tarjan求强连通分量用low还是dfn来更新?有区别吗?
原文:https://www.cnblogs.com/JWizard/p/13273903.html