文章发表在KDD 2018 Research Track上,链接为Modeling Task Relationships in Multi-task Learning with Multi-gate Mixture-of-Experts。
多任务学习可被用在许多应用上,如推荐系统。如在电影推荐中,用户可购买和喜欢观看偏好的电影,故可同时预测用户购买量以及对电影的打分。
多任务学习常对任务之间的相关性较敏感,故权衡任务之间的目标以及任务内部关系十分重要。
MMOE模型可用来学习任务之间的关系,本文采用MOE(专家模型)在多个任务之间通过共享专家子网络来进行多任务学习,其中设置一个门结构来训练优化每个任务。
多任务模型通过学习不同任务的联系和差异,可提高每个任务的学习效率和质量。
(1)多任务学习的的框架广泛采用shared-bottom的结构,不同任务间共用底部的隐层。
这种结构本质上可以减少过拟合的风险,但是效果上可能受到任务差异和数据分布带来的影响。
(2)也有一些其他结构,比如两个任务的参数不共用,但是通过对不同任务的参数增加L2范数的限制;也有一些对每个任务分别学习一套隐层然后学习所有隐层的组合。
和shared-bottom结构相比,这些模型对增加了针对任务的特定参数,在任务差异会影响公共参数的情况下对最终效果有提升。
缺点就是模型增加了参数量所以需要更大的数据量来训练模型,而且模型更复杂并不利于在真实生产环境中实际部署使用。
因此,论文中提出了一个Multi-gate Mixture-of-Experts(MMoE)的多任务学习结构。MMoE模型刻画了任务相关性,基于共享表示来学习特定任务的函数,避免了明显增加参数的缺点。
MMoE模型的结构(下图c)基于广泛使用的Shared-Bottom结构(下图a)和MoE结构,其中图(b)是图(c)的一种特殊情况。
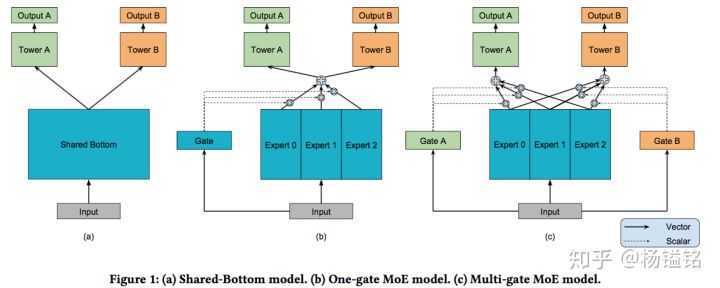
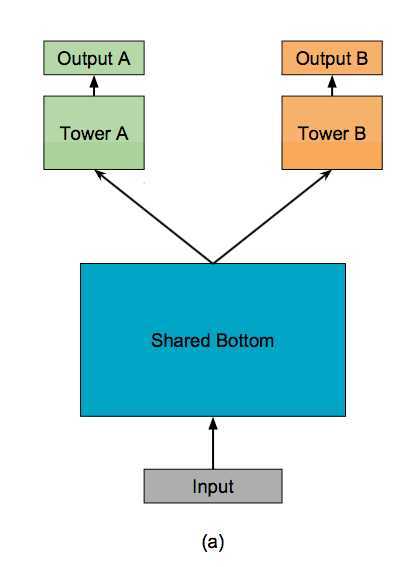
如上图a所示,shared-bottom网络(表示为函数f)位于底部,多个任务共用这一层。往上,K个子任务分别对应一个tower network(表示为 ),每个子任务的输出
。
接下来,我们通过一个实验来探讨任务相关性和多任务学习效果的关系。
假设模型中包含两个回归任务,而数据通过采样生成,并且规定输入相同,输出label不同。那么任务的相关性就使用label之间的皮尔逊相关系数来表示,相关系数越大,表示任务之间越相关,数据生成的过程如下:

首先,生成了两个垂直的单位向量u1和u2,并根据两个单位向量生成了模型的系数w1和w2,如上图中的第二步。w1和w2之间的cosine距离即为p,大伙可以根据cosine的计算公式得到。
随后基于正态分布的到输入数据x,而y根据下面的两个式子的到:

注意,这里x和y之间并非线性的关系,因为模型的第二步是多个sin函数,因此label之间的皮尔逊相关系数和参数w1和w2之间的cosine距离并不相等,但是呈现出一个正相关的关系,如下图:

因此,本文中使用参数的cosine距离来近似表示任务之间的相关性。
基于上述数据生成过程以及任务相关性的表示方法,分别测试任务相关性在0.5、0.9和1时的多任务学习模型的效果,如下图:

可以看到的是,随着任务相关性的提升,模型的loss越小,效果越好,从而印证了前面的猜想。
先来看一下Mixture-of-Experts (MoE)模型(文中后面称作 One-gate Mixture-of-Experts (OMoE)),如下图所示:
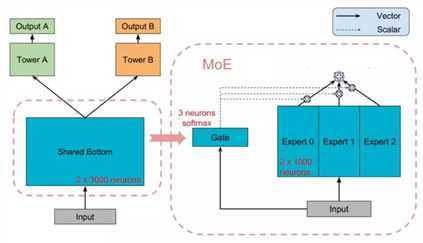
可以看到,相较于一般的多任务学习框架,共享的底层分为了多个expert,同时设置了一个Gate,使不同的数据可以多样化的使用共享层。此时共享层的输出可以表示为:

其中fi代表第i个expert的输出, 是n个expert network(expert network可认为是一个神经网络),gi代表第第i个expert对应的权重,是基于输入数据得到的,计算公式为g(x) = softmax(Wgx),其中
。g是组合experts结果的gating network,具体来说g产生n个experts上的概率分布,最终的输出是所有experts的带权加和。显然,MoE可看做基于多个独立模型的集成方法。
后面有些文章将MoE作为一个基本的组成单元,将多个MoE结构堆叠在一个大网络中。比如一个MoE层可以接受上一层MoE层的输出作为输入,其输出作为下一层的输入使用。
文章提出的模型(简称MMoE)目的就是相对于shared-bottom结构不明显增加模型参数的要求下捕捉任务的不同。其核心思想是将shared-bottom网络中的函数f替换成MoE层
相较于MoE模型,Multi-gate Mixture-of-Experts (MMoE)模型为每一个task设置了一个gate,使不同的任务和不同的数据可以多样化的使用共享层,模型结构如下:

此时每个任务的共享层的输出不同,第k个任务的共享层输出计算公式如下:

随后每个任务对应的共享层输出,经过多层全连接神经网络得到每个任务的输出:

从直观上考虑,如果两个任务并不十分相关,那么经过Gate之后,二者得到的权重系数会差别比较大,从而可以利用部分expert网络输出的信息,近似于多个单任务学习模型。如果两个任务紧密相关,那么经过Gate得到的权重分布应该相差不多,类似于一般的多任务学习框架。
相对于所有任务公共一个门控网络(One-gate MoE model,如上图b),这里MMoE(上图c)中每个任务使用单独的gating networks。每个任务的gating networks通过最终输出权重不同实现对experts的选择性利用。不同任务的gating networks可以学习到不同的组合experts的模式,因此模型考虑到了捕捉到任务的相关性和区别。
网络中export是切分的子网络,实现的时候其实可以看做是三维tensor,形状为:
dim of input feature * number of units per expert * number of experts
更新时是对这个三维tensor进行更新。
gate的形状则为:
dim of input feature * number of experts * number of tasks
然后一点网络中的小小小details,贴在这里可以参考一下,帮助理解:
f_{i}(x) = activation(W_{i} * x + b), where activation is ReLU according to the paper
g^{k}(x) = activation(W_{gk} * x + b), where activation is softmax according to the paper
f^{k}(x) = sum_{i=1}^{n}(g^{k}(x)_{i} * f_{i}(x))
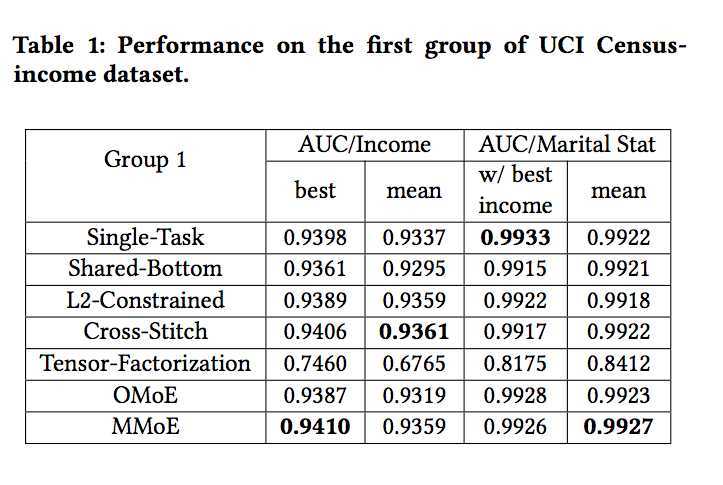
下图是实验结果,OMoE是单门MoE。可以看到在相关性强的数据上,OMoE和MMoE差别不大,但是在相关性低的数据上,MMoE胜过其他两个方法很多。
https://zhuanlan.zhihu.com/p/55752344
https://zhuanlan.zhihu.com/p/96796043
多任务学习模型详解:Multi-gate Mixture-of-Experts(MMoE ,Google,KDD2018)
原文:https://www.cnblogs.com/Lee-yl/p/13274401.html