第八章——排序

一、基本概念

有n个记录的序列{R1，R2，…，Rn}，其相应关键字的序列是{K1，K2， …，Kn }，相应的下标序列为1，2，…，n。
通过排序，要求找出当前下标序列1，2，…， n的一种排列p1，p2， …，pn，使得相应关键字满足如下的**非递减（或非递增）**关系，

即：Kp1≤ Kp2≤…≤ Kpn ，就得到一个按关键字有序的记录序列：{Rp1，Rp2， …， Rpn}。

（1）内部排序与外部排序。
内部排序：整个排序过程不需要访问外存便能完成
外部排序：参加排序的记录数量很大，整个序列的排序过程不可能在内存中完成，需要借助外存
（2）主关键字与次关键字
上面所说的关键字  Ki 可以是记录 i 的主关键字，也可以是次关键字，甚至可以是记录中若干数据项的组合。
若Ki是主关键字，则任何一个无序的记录序列经排序后得到的有序序列是唯一的。若Ki是次关键字或是记录中若干数据项的组合，得到的排序结果将是不唯一的，因为待排序记录的序列中存在两个或两个以上关键字相等的记录。
（3）排序的稳定性
若两个记录A和B的关键字值相等，若排序后A、B的先后次序保持不变，则称这种排序算法是稳定的，反之称为不稳定的。
（4）算法的优劣性
  时间效率：排序速度(排序所花费的全部比较次数)
  空间效率：占内存辅助空间的大小
  稳定性：排序是否稳定
注：本章均以升序排序为例。

二、基本排序方法

1. 插入排序

基本思想： 在一个已排好序的记录子集的基础上，每一步将下一个待排序的记录有序插入到已排好序的记录子集中，直到将所有待排记录全部插入为止。

1.1 直接插入
算法思想： 将第i个记录插入到前面i-1个已排好序的记录中。
具体过程： 将第i个记录的关键字Ki，顺次与其前面记录的关键字Ki-1，Ki-2，…, K1进行比较，将所有关键字大于Ki的记录依次向后移动一个位置，直到遇见一个关键字小于或者等于Ki的记录Kj，此时Kj后面必为空位置，将第i个记录插入空位置即可。
时间复杂度O(n2)。
O(n2),空间复杂度为O(1)O(1)，直接插入排序是一种稳定的排序方法。

 1 void insertSort(int[] a, int len) {
 2     for (int i = 0; i < len; i++) {
 3         int j = i - 1, temp = a[i];
 4 
 5         while (j >= 0 && temp < a[j]) {
 6             a[j + 1] = a[j];
 7             j--;
 8         }
 9         a[j + 1] = temp;
10     }
11 }

直接插入

1.2 折半插入

算法思想： 在已形成的有序表中折半查找，并在适当位置插入，把原来位置上的元素向后顺移。

折半查找相比与插入排序比较的次数大大减少，全部元素比较次数仅为 O(nlogn) 。但其并未改变移动元素的时间耗费，

所以时间效率仍然为为O(n^2) ，空间效率为O(1) ,折半插入也是一种稳定的排序方法。

1.3希尔排序

算法思想： 先将整个待排记录序列分割成若干子序列, 分别进行直接插入排序, 待整个序列中的记录“基本有序”时，再对全体记录进行一次直接插入排序。

技巧： 子序列的构成不是简单地“逐段分割”，而是将相隔某个增量dk的记录组成一个子序列。关于增量 d 的取法，最初提出取d=n/2，d=d/2，直到d=1为止。该思路的缺点是，在奇数位置的元素在最后一步才会与偶数位置的元素进行比较，使得希尔排序效率降低。因此后来提出d=d/3+1。

时间效率因为选取的增量的不同而不同，空间效率为O（1），希尔排序是一种不稳定的排序。

 1 void shellSort(int[] a, int len) {
 2     for (int h = len / 2; h > 0; h /= 2) {
 3         for (int i = h; i < len; i++) {
 4             int temp = a[i];
 5             int j = i - h;
 6             for (; j >= 0; j -= h) {
 7                 if (temp < a[j]) {
 8                     a[j + h] = a[j];
 9                 } else {
10                     break;
11                 }
12             }
13             a[j + h] = temp;
14         }
15     }
16 }

希尔排序

2.交换排序

1.冒泡排序

冒泡排序是一种简单的交换类排序方法，它是通过相邻的数据元素的交换，逐步将待排序序列变成有序序列的过程。

算法思想： 每趟对所有记录从左到右相邻两个记录进行比较，若不符合排序要求，则进行交换。使用前提必需是顺序存储结构。

时间效率为 O（n2），空间效率为O（1），冒泡排序是一种稳定的排序。

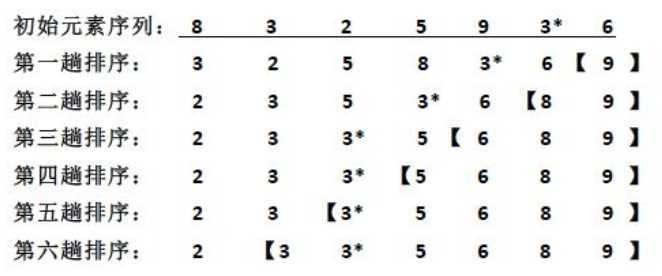
若序列为{8, 3, 2, 5, 9, 3, 6}，下图给出排序过程：

 1 void bubbleSort(int[] a, int len) {
 2     for (int i = 0; i < len - 1; i++) {
 3         for (int j = 0; j < len - 1 - i; j++) {
 4             if (a[j] > a[j + 1]) {
 5                 int temp = a[j];
 6                 a[j] = a[j + 1];
 7                 a[j + 1] = temp;
 8             }
 9         }
10     }
11 }

冒泡排序

2.快速排序
改进要点： 在冒泡排序中，由于扫描过程中只对相邻的两个元素进行比较，因此在互换两个相邻元素时只能消除一个逆序。如果能通过两个（不相邻的）元素的交换，消除待排序记录中的多个逆序，则会大大加快排序的速度。快速排序方法中的一次交换可能消除多个逆序。
算法思想： 从待排序列中任取一个元素 (例如取第一个) 作为中心，所有比它小的元素一律前放，所有比它大的元素一律后放，形成左右两个子表；然后再对各子表重新选择中心元素并依此规则调整，直到每个子表的元素只剩一个。此时便为有序序列了。
快速排序的使用前提也是顺序存储结构，快速排序的最差时间复杂度和冒泡排序是一样的都是O(n2)
O(n2)，它的平均时间复杂度为O(nlogn)O(nlogn)，是一种不稳定的排序方法。

参考博客：https://www.cnblogs.com/ahalei/p/3568434.html

                  https://blog.csdn.net/yuanlaijike/article/details/78078434

 1 void quickSort(int[] a, int left, int right) {
 2     if (left > right) {
 3         return;
 4     }
 5 
 6     // 基数
 7     int temp = a[left];
 8     int i = left, j = right;
 9 
10     while (i != j) {
11         // 先从右边开始左移
12         while (a[j] >= temp && i < j) {
13             j--;
14         }
15         // 再从左边开始右移
16         while (a[i] <= temp && i < j) {
17             i++;
18         }
19 
20         // 交换元素
21         if (i < j) {
22             int t = a[i];
23             a[i] = a[j];
24             a[j] = t;
25         }
26     }
27 
28     // 基数和相交点交换
29     a[left] = a[i];
30     a[i] = temp;
31 
32     // 拆分成两个子队列递归
33     quickSort(a, left, i - 1);
34     quickSort(a, i + 1, right);
35 }

快速排序

3.选择排序

在待排记录中依次选择关键字最小的记录作为有序序列的最后一条记录，逐渐缩小范围直至全部记录选择完毕。

3.1 简单选择排序

算法思想： 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。

时间复杂度O（n2），空间复杂度为O（1），简单排序为不稳定。

 1 void selectSort(int[] a, int len) {
 2     for (int i = 0; i < len - 1; i++) {
 3         int min = i;
 4         for (int j = i + 1; j < len; j++) {
 5             if (a[min] > a[j]) {
 6                 min = j;
 7             }
 8         }
 9         if (min != i) {
10             int temp = a[min];
11             a[min] = a[i];
12             a[i] = temp;
13         }
14     }
15 }

简单选择排序

3.2 树型选择排序

算法思想： 把带排序的n个记录的关键字两两进行比较，取出较小者。在[n/2]个较小者中，采用同样的方法进行比较选出每两个中的较小者。如此反复，

直至选出最小关键字记录为止。树型选择排序又称为锦标赛法，时间复杂度O（nlogn），空间复杂度为O（n）O(nlogn)

树型选择排序是一种稳定的排序方法。相较于简单选择排序，虽然提升了时间复杂度，但是增加了空间复杂度，其本质是空间换时间。

3.3 堆排序

算法思想： 把待排序数组看成一颗完全二叉树，结点r[i]的左孩子是r[2i]，右孩子是r[2i+1]，双亲是r[i/2]。

通过调整完全二叉树建堆及重建堆选择出关键字最小记录及次小记录等实现排序。

首先介绍下堆、小根堆和大根堆的概念：

    堆(Heap)：每个结点的值都大于、小于或等于其左右孩子结点的值
   小根堆：每个结点的值都小于或等于其左右孩子结点的值
    大根堆：每个结点的值都大于或等于其左右孩子结点的
时间复杂度：T(n)=O(nlogn)，空间复杂度：S(n)=O(1)，堆排序是一种不稳定的排序方法。
以大根堆为例，首先我们根据堆定义建立初堆。去掉最大元之后重建堆，得到次大元。如此类推，完成堆排序。
建初堆步骤：
将一个任意序列看成是对应的完全二叉树，筛选需从最后一个子树位置[n/2]开始，反复利用重建堆法自底向上，把所有子树逐层调整为堆，直至根节点。
重建堆步骤：：
1）将完全二叉树根结点中的关键字x移出，此时根结点相当于空结点。
2）从空结点的左、右子中选出关键字最大的记录，如果该记录的关键字大于x，则将该记录上移至空结点。
3）重复上述移动过程，直到空结点左、右子的关键字均不大于x。此时，将待调整记录放入空结点即可。
重建堆的调整方法相当于把待调整记录逐步向下“筛”的过程，所以一般称为筛选。
堆排序步骤：
1）建立初堆：从最后一子树n/2直到根建堆。
2）将堆顶第一个元素与最后一个元素互换。
3）去掉最后元素，将剩余元素调整建堆，再转出堆顶元素。

4）重复执行（2）、（3）步骤n−1次，直到序列有序。

 1  void heapSort(int[] a, int len) {
 2     // 建立出堆
 3     for (int i = len / 2 - 1; i >= 0; i--) {
 4         adjustHeap(a, i, len - 1);
 5     }
 6     
 7     // 交换首末元素,并重建堆
 8     for (int i = len - 1; i >= 0; i--) {
 9         int temp = a[0];
10         a[0] = a[i];
11         a[i] = temp;
12         adjustHeap(a, 0, i - 1);
13     }
14 }
15  void adjustHeap(int[] a, int pos, int len) {
16     int temp, child;
17     for (temp = a[pos]; 2 * pos + 1 <= len; pos = child) {
18         child = 2 * pos + 1;
19         if (child < len && a[child] < a[child + 1]) {
20             child++;
21         }
22         if (a[child] > temp) {
23             a[pos] = a[child];
24         } else {
25             break;
26         }
27     }
28     a[pos] = temp;
29 }

堆排序

3.归并排序

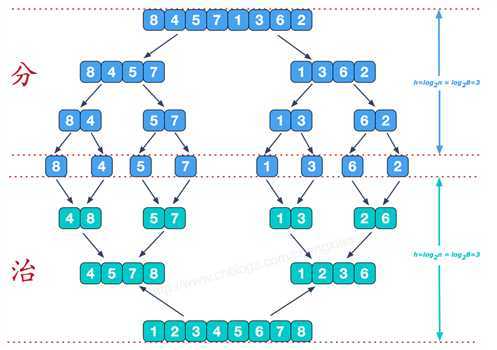
算法思想： 假设初始序列含有 n 个记录，首先将这 n 个记录看成 n 个有序的子序列， 每个子序列的长度为 1，然后两两归并，得到[2/n]个长度为 2（n 为奇数时，最后一个序列的长度为 1）的有序子序列。在此基础上，再对长度为2的有序子序列进行两两归并，得到若干个长度为4的有 序子序列。如此重复，直至得到一个长度为 n的有序序列为止。
归并排序总的时间复杂度为 O(nlogn)，在实现归并排序时，需要和待排记录等数量的辅助空间，空间复杂度为 O(n) ，归并排序是一种稳定的排序方法。

 1 void mergeSort(int[] a, int left, int right, int[] temp) {
 2     if(left < right) {
 3         int mid = (left + right) / 2;
 4 
 5         //左边归并排序,使得左子序列有序
 6         mergeSort(a, left, mid, temp);
 7         //右边归并排序,使得右子序列有序
 8         mergeSort(a, mid + 1, right, temp);
 9         //将两个有序子数组合并操作
10         merge(a, left, mid, right, temp);
11     }
12 }
13 void merge(int[] a, int left, int mid, int right, int[] temp) {
14     // 左指针、右指针、temp数组指针
15     int i = left, j = mid + 1, t = 0;
16 
17     // 依次比较填充temp数组
18     while (i <= mid && j <= right) {
19         if(a[i] < a[j]) {
20             temp[t++] = a[i++];
21         } else {
22             temp[t++] = a[j++];
23         }
24     }
25 
26     // 将剩余未拷贝的元素拷贝到temp数组
27     while (i <= mid) {
28         temp[t++] = a[i++];
29     }
30     while (j <= right) {
31         temp[t++] = a[j++];
32     }
33 
34     // 将temp数组中元素拷贝回原始数组
35     t = 0;
36     while (left <= right) {
37         a[left++] = temp[t++];
38     }
39 }

归并排序

三、总结

 元素的移动次数与关键字的初始排列次序无关的是：基数排序。
元素的比较次数与初始序列无关是：选择排序。
算法的时间复杂度与初始序列无关的是：直接选择排序

自动判断 中文 中文(简体) 中文(香港) 中文(繁体) 英语 日语 朝鲜语 德语 法语 俄语 泰语 南非语 阿拉伯语 阿塞拜疆语 比利时语 保加利亚语 加泰隆语 捷克语 威尔士语 丹麦语 第维埃语 希腊语 世界语 西班牙语 爱沙尼亚语 巴士克语 法斯语 芬兰语 法罗语 加里西亚语 古吉拉特语 希伯来语 印地语 克罗地亚语 匈牙利语 亚美尼亚语 印度尼西亚语 冰岛语 意大利语 格鲁吉亚语 哈萨克语 卡纳拉语 孔卡尼语 吉尔吉斯语 立陶宛语 拉脱维亚语 毛利语 马其顿语 蒙古语 马拉地语 马来语 马耳他语 挪威语(伯克梅尔) 荷兰语 北梭托语 旁遮普语 波兰语 葡萄牙语 克丘亚语 罗马尼亚语 梵文 北萨摩斯语 斯洛伐克语 斯洛文尼亚语 阿尔巴尼亚语 瑞典语 斯瓦希里语 叙利亚语 泰米尔语 泰卢固语 塔加路语 茨瓦纳语 土耳其语 宗加语 鞑靼语 乌克兰语 乌都语 乌兹别克语 越南语 班图语 祖鲁语 自动选择 中文 中文(简体) 中文(香港) 中文(繁体) 英语 日语 朝鲜语 德语 法语 俄语 泰语 南非语 阿拉伯语 阿塞拜疆语 比利时语 保加利亚语 加泰隆语 捷克语 威尔士语 丹麦语 第维埃语 希腊语 世界语 西班牙语 爱沙尼亚语 巴士克语 法斯语 芬兰语 法罗语 加里西亚语 古吉拉特语 希伯来语 印地语 克罗地亚语 匈牙利语 亚美尼亚语 印度尼西亚语 冰岛语 意大利语 格鲁吉亚语 哈萨克语 卡纳拉语 孔卡尼语 吉尔吉斯语 立陶宛语 拉脱维亚语 毛利语 马其顿语 蒙古语 马拉地语 马来语 马耳他语 挪威语(伯克梅尔) 荷兰语 北梭托语 旁遮普语 波兰语 葡萄牙语 克丘亚语 罗马尼亚语 梵文 北萨摩斯语 斯洛伐克语 斯洛文尼亚语 阿尔巴尼亚语 瑞典语 斯瓦希里语 叙利亚语 泰米尔语 泰卢固语 塔加路语 茨瓦纳语 土耳其语 宗加语 鞑靼语 乌克兰语 乌都语 乌兹别克语 越南语 班图语 祖鲁语 有道翻译 百度翻译 谷歌翻译 谷歌翻译（国内） 翻译 朗读 复制 正在查询，请稍候…… 重试 朗读 复制 复制 朗读 复制 via 谷歌翻译（国内）译

数据结构第8章小结

原文：https://www.cnblogs.com/apiao127/p/13283243.html