今天又把KMP算法看了一遍,特此小结。
扯淡的话:
KMP算法主要用来模式匹配。正如Implement strStr() 中形容的一样,“大海捞针”,当时看到题中变量如此命名,真的感觉实在是再贴切不过了。
在介绍KMP算法之前,先介绍一下BF算法,叫的这么暧昧(who is GF?),其实就是最low的暴力算法。这个男票略暴力。
事实上,JDK1.7中String的contains的源码用的就是BF算法。(1.7中调用了indexOf,我记得1.6中是直接写的contains接口来着)
截取了一部分,并稍稍改动一下下

public boolean contains(String p){ char[] source ; char[] target = p.toCharArray(); char fist = p.charAt(0); int end = p.length() ; int max = s.length() - 1; for (int i = 0; i <= max; i++) { /* Look for first character. */ if (source[i] != first) { while (++i <= max && source[i] != first); } /* Found first character, now look at the rest of v2 */ if (i <= max) { int j = i + 1; int end = j + targetCount - 1; for (int k = 1; j < end && source[j] == target[k]; j++, k++); if (j == end) { /* Found whole string. */ return true; } } } return false; }
可能网上很多实现不太一样,但是总体的算法思路都相同。看不懂也不要紧,因为看懂也不会有人问你这个。模式匹配算法是非常实用的算法之一,例如论文查重,字符串的模式匹配就是其中一种实现,虽然现在已经有更高大上的“树匹配” 和 “图匹配” 了,但是文本匹配也是一个非常重要的应用。BF算法是模式匹配中最low的算法时间之一,复杂度是O(m*n),这是非常恐怖的,试想,论文查重将你的论文与数据库中所有论文进行匹配.....准备延毕吧。因此BF算法貌似并没有太大的应用价值。
下面来看KMP算法,这是一个线性算法,复杂度是O(n + m)【一般情况下,n >> m,因此你也可以说是O(n)】,同AVL树一样,KMP算法的命名是由Knuth、Morris、Pratt三位作者的首字母组成的。不再多说。
在开讲之前,首先要来了解该算法中应用的几个概念:前缀 & 后缀
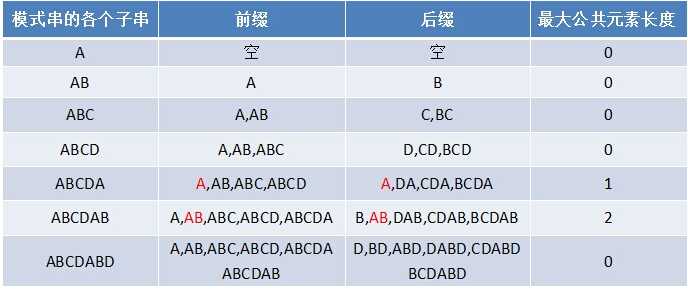
其实看到前缀、后缀字眼大家就能猜到是啥意思,但是对于KMP来讲,这里的前缀和后缀指的是绝对前缀、绝对后缀。不能包含其自身。
还是看图说话吧。
这里我就不讲了,大家先仔细看图说话





这里发现了不一致,BF算法是酱紫的:

但是仔细观察会发现,其实不必要,可以这样:

再对比一下这两种情况:(上下为一组)




你会发现:BF回溯了 而KMP,相对于字符串s而言,是一路向前的,因此,从这里粗略来看,时间复杂度是O(n)。
这里我们开始编码,即:遇到不同的字符,s的指针不变,p向右移动x个位置,这个x到底是多少,这里先不管,一会儿再讲。
while(i < s.length()){ if(p.charAt(j) == s.charAt(i)){ i++; j++; }else{ j = next[j];//这里这个next[j]表示上面说的x个位置 } if(j == p.length()) return i - p.length(); }
具体的代码框架应该是这样的,当两个字符相同时,继续比较s和p的下一个位置,如果不同,i不变,j向右移动next[j]步。当j == p.length 的时候,即表示在s中找到了一个子串为p。因此返回其实下标。
好了,回到问题的核心,这个x,具体是多少。还记得上面讲的前缀后缀吗?没错,这里要用到。
再来看这个图:

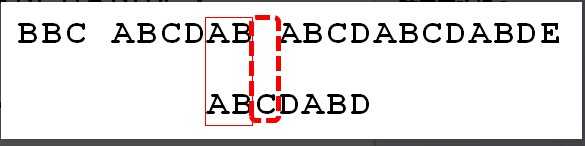
图中在上面虚线框处(当前s的下标是10)发生了失配,然后我们把p移动了x个位置(本例中,x == 4),到了下图的虚线框,现在有没有意识到为什么要移动x个位置,而不是x + 1或者x - 1个位置了吧?注意实线框。
还不明白?
KMP算法比BF算法高效的一点就是,s只需要一路向前,不能回溯,当发生失配时,为保证s的下标指针 i 不回溯,那么就要保证 i 之前的元素要么与p匹配,或者为空。因此这里移动了x个位置,使得虚线框之前的子串与p匹配。如果还不明白,那就去看july的博客吧,上面讲的炒鸡详细。
再看p
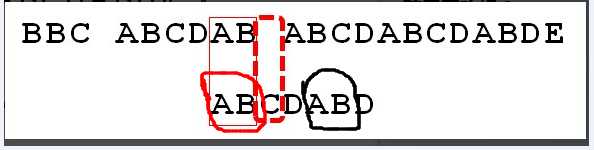
第一次匹配的是我用黑圈围起来的AB,移动之后匹配的是红圈围起来的AB,这两个AB对 “D之前的子串” 来讲是什么东东?bingo:前缀 & 后缀 啊!准确来讲,是 最长前缀 和 最长后缀 。
有点明白了吧?
移动的距离其实是与 最长匹配前后缀 的长度有关的。
例如上图中ABCDABD中的D,其最长相等前后缀是AB,长度为2,因此将p.charAt(2)移动到虚线框的位置,并从这里往后比较。
因此这里就可以看出上段代码中的 next[j] 实际上只与字符串p中的 j 相关,与s并无关系。
然而,next数组,该如何得到呢?
首先结合上面的图片来确认一下next数组表达的含义:
next[j]的值表示p[0 ~ j - 1]中最长匹配前后缀的长度。(所谓匹配前后缀是指:前缀.equals(后缀))
如上图中的
ABCDAB D
next 2
即表示:p[0 ~ j - 1]即ABCDAB:其前缀有:A 、AB、ABC、ABCD、ABCDA
其后缀有: B、AB、DAB、CDAB、BCDAB
很容易看出:最长匹配前后缀是AB,长度为2,因此next[6] = 2;
特别的,约定next[0] = -1;
这样看来,next数组直接求解是很容易的,只需要对每一个子串的所有前后缀进行检查即可。然而,这个复杂度最小也是O(m^2),可以优化:
递推版本:由next[0 ~ i - 1],求出next[i]
算法思想:假设next[j] = k,即:P[0..k - 1] = P[j - k .. j - 1](前k个,后k个相等)
根据定义next[0] = - 1。(下面是摘自海子版的递推公式)
1) 如P[j] = P[k],因此P[0 ~ k] = P[j - k ~ j]:即有next[j + 1] = next[j] + 1 = k + 1;
2) 如P[j] != P[k],则可以把其看做模式匹配问题,即匹配失败的时候,k值如何移动,显然k = next[k]。
我智商比较拙计,怎么“显然”:而且P[j] = P[k] => next[j + 1] = next[j] + 1 = k + 1,是如何保证P[0..k - 1] = P[j - k .. j - 1] 的?
这里,我简单的将二者给解释一下:
关于第一点:
如P[j] = P[k],因此P[0 ~ k] = P[j - k ~ j]:即有next[j + 1] = next[j] + 1 = k + 1;
在求next[j]时,已经能确保此时k的值是 k = next[j - 1];不明白?请点击下面展开

当你求next[j]的时候,是不是上一步刚刚求过next[j - 1] ? 即next[j - 1] = k 这说明什么? 是不是说明p[0 ~ k - 1] = p[j - k, j - 1]?
这里有一种特殊情况,即当k = -1时,next[j] = 0(注意:k = -1 时,并不一定以为着仅仅在求next[1]时用到,下面就会讲到)
第二点:
如P[j] != P[k],则可以把其看做模式匹配问题,即匹配失败的时候,k值如何移动,显然k = next[k]。
“显然” 这两个字用的感觉有点推卸责任,但是没关系,自己剖析一下:
来看这个栗子:当前状态为:
k j
↓ ↓
a b a b a a b e
next -1 0 0 1 2 3
此时已知的条件有,红色字体标记的前缀和绿色阴影标记的后缀是最长匹配的,k= 3,j = 5,现在求b的next值
如果这里p[j] == p[k],那么很好办了,b直接next[j + 1] = next[j] + 1 = k + 1 = 4;这里可以很直观的看出,为什么next[j + 1] = next[j] + 1;
可惜这里p[j] != p[k],肿么办?按照上面的算法:k = next[k],即k = 1;然后再比较p[1] ? p[j],如果还不相等,继续k = next[k];
为什么?当你没有思路的时候,回到起点吧,定义是普适的。
首先俩看下next[k]表示什么意义?k之前的子串的最长匹配,即表示b之前的aba子串的最长匹配。
因此这里的next[k] = 1表示的是aba中的最长匹配前缀(后缀)长度为1,即next[k]表示红色字体标记的前缀 的最长前缀
而我们在不断的k = next[k],是为了寻找什么?是为了找b之前的最长前缀啊,找到了又怎样?还要跟后缀匹配啊!
进一步剖析一下b之前的子串 a b a b a a(将其命名为sub)
我们要找这个子串的最长匹配前后缀,首先我们已经确定了,后缀的最一个字母是a,先不看这个a,继续往前看, a b a。如果sub的后缀长度 > 1的话,倒数第2个字符一定是a,倒数第3个一定是b,倒数第4个一定是a,有没有倒数第5个? 不可能!!因为如果有倒数第5个字符的话,那么a b a b a 的最长匹配前后缀的长度至少是4,先把这个理解了再往下看吧。
即next[j + 1] <= next[j] + 1。
再来看sub : a b a b a a
继续不看最后的a,看前面的 a b a b a 我们要找这里面的最长匹配前后缀,只有在这个子串中匹配了,才可能在sub中匹配
又回到了原点:a b a是这里的一个前缀,a b a ,此时k 指向了前缀的下一个字符b,后缀的下一个字符是a,不匹配,再继续寻找,怎么找?k = next[k]
注意,next[k]表示啥?上面说过了,表示红色字体标记的 字符串的 最长前缀。同时。也表示:红色字体标记的字符串的最长匹配后缀。
再观察一下发现:红色字体跟绿色阴影是完全相等的,那么红色字体标记的前缀,岂不是就等于绿色阴影的后缀了吗?
因此每一次next[k]其实是在红色字体中 寻找 与 绿色阴影后缀 匹配的 前缀啊!比较拗口,理解了再往下看。
每查找一下,k都指向前缀后面的字符,然后将其与a作比较,如果相等,则next[j + 1] = k + 1;否则要继续往前找合适的前缀,最极端的情况就是:直到p[0],发现p[0] != p[j],next[j] = 0。
理解到这里,再看代码,将next[0]初始化为-1 ,并与p[j] = p[k]的处理合并到一起,实在是太巧妙了。。
分析到这里,就可以看代码了
public void setNext(String m,int[] next){ char[] s = m.toCharArray(); int length = m.length(), j = 0, k = -1; next[0] = -1; while(j < length - 1){//注意这里是length - 1,原因自己理解 if(k == - 1 || s[j] == s[k]){//将k = -1与s[j] = s[k]放一起处理了,看起来好优美 next[++j] = ++k; }else{ k = next[k]; } } }
这里就得到了next数组
再来看怎么用next数组。
刚才的图:


上面的setNext运行过后,匹配到D时候,发生失配,此时next[6] = 2,因此我们将i不变,j = next[j],让空格与C继续匹配。
ABCDAB D
next 2
代码如下:
public int match(String s,String p){ int[] next = new int[p.length()]; int i = 0 , j = 0; setNext(p, next); while(i < s.length()){ if(j == -1 || p.charAt(j) == s.charAt(i)){//这里j = -1 的处理其实跟上面setNext有异曲同工之妙的,你体会一下 i++; j++; }else{//失配时,j = next[j] j = next[j]; } if(j == p.length()) return i - p.length(); } return -1; }
合并之后的代码:附test case

1 package Algorithme; 2 3 import java.util.ArrayList; 4 import java.util.List; 5 6 public class KMP { 7 public void setNext(String m,int[] next){ 8 char[] s = m.toCharArray(); 9 int length = m.length(), j = 0, k = -1; 10 next[0] = -1; 11 while(j < length - 1){ 12 if(k == - 1 || s[j] == s[k]){ 13 next[++j] = ++k; 14 }else{ 15 k = next[k]; 16 } 17 } 18 } 19 public int match(String s,String p){ 20 int[] next = new int[p.length()]; 21 int i = 0 , j = 0; 22 setNext(p, next); 23 while(i < s.length()){ 24 if(j == -1 || p.charAt(j) == s.charAt(i)){ 25 i++; 26 j++; 27 }else{ 28 j = next[j]; 29 } 30 if(j == p.length()) return i - p.length(); 31 } 32 return -1; 33 } 34 35 public static void main(String[] args) { 36 KMP test = new KMP(); 37 List<String> list = new ArrayList<String>(); 38 String s1 = "i love qiqi"; 39 String s2 = "qiqi is my girl friend"; 40 String s3 = "we have been together for five years"; 41 list.add(s1); 42 list.add(s2); 43 list.add(s3); 44 String p = "qiqi"; 45 for(String s : list) 46 System.out.println(test.match(s, p)); 47 } 48 }
截止到这里,KMP算法基本算解释完了,如果没听懂,欢迎留言讨论。
参考资料:
July版:http://blog.csdn.net/v_july_v/article/details/7041827(优点,很详细。缺点:太啰嗦;吐槽:他的书肯定很厚,很贵 ̄へ ̄)
海子版:http://www.cnblogs.com/dolphin0520/archive/2011/08/24/2151846.html?ADUIN=313359714&ADSESSION=1410660113&ADTAG=CLIENT.QQ.5353_.0&ADPUBNO=26381(优点:很精练,缺点:有的地方一笔带过,太糙)
OI版:http://www.matrix67.com/blog/archives/115(以一种非主流的方式讲了KMP,很厉害,据说是作者当时是一名高中生)
原文:http://www.cnblogs.com/huntfor/p/3971261.html