第八章我们学习了排序,下面是我们学习的主要框架
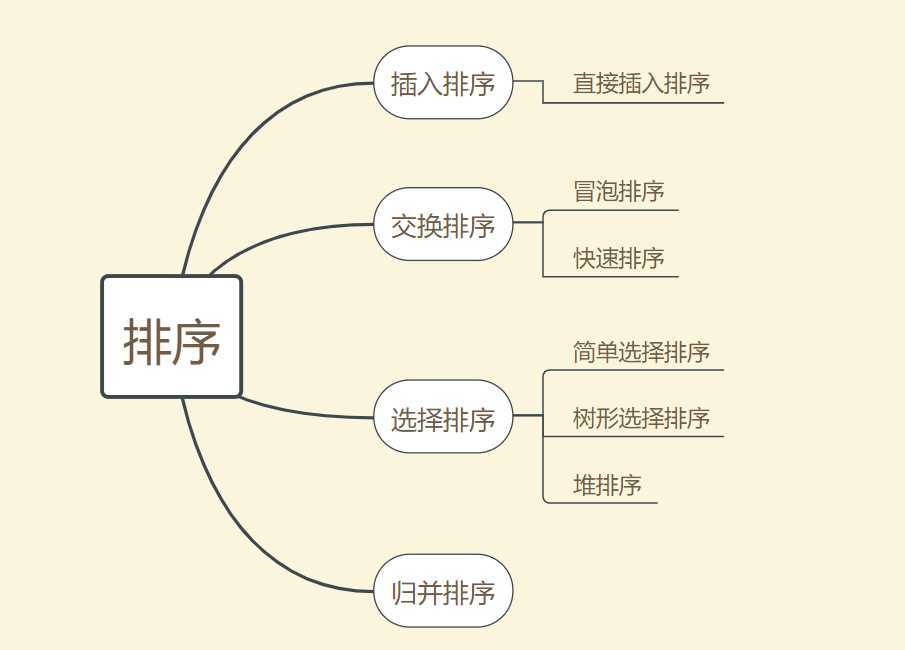
排序分为内部排序和外部排序,我们学习的主要是上面所提及的内部排序的几种。
在分析排序时间复杂度时,不同于以往的分析,我们不仅要关注比较次数,还要关注移动次数。
(下面默认排序是按非递减)
| 排序 | 算法概述 | 时间复杂度 | 空间复杂度 | 算法特点 |
| 直接插入排序 |
1.在r[0]设置监视哨 2.将待排序的放进数组r[1...n],r[1]是个有序数组 3.顺序查找法查找r[2]在有序数组合适的位置,插入,有序数组元素个数加一 4.顺序查找法查找r[3]在有序数组合适的位置,插入,有序数组元素个数加一 5.重复上述步骤直到r[n]被插入到表长为n-1的有序数组 |
O(n^2) |
只需要一个辅助空间r[0] 所以为O(1) |
1.稳定排序 2.算法简便,容易实现 3.也适合链式存储结构,在单链表无需移动,只需修改相应指针 4.更适合初始状态有序的情况 |
| 冒泡排序 |
1.将待排序记录存放r[1...n] 2.比较r[2]、r[1],若逆序则交换两个数的顺序 3.比较r[3]、r[2],若逆序则交换两个数的顺序,若交换了记录,再比较r[2]、r[1], 若逆序则交换两个数的顺序 4.重复上述步骤,将r[i]r[i-1],比较,若逆序则交换位置,再将r[i-1]r[i-2]比较,直到两个数比较无逆序为止,停止比较,退出循环 5.将r[n]与前面的记录比较,当循环结束得到一个长度为n的有序表 |
O(n^2) | 只在交换时需要一个辅助空间,所以为O(1) |
1.稳定排序 2.可用于链式存储结构 3.移动次数较多,算法平均时间性能比直接插入差。当初始记录无序,n较大,不适用 |
| 快速排序 |
1.将待排序表第一个记录作为枢轴,暂存r[0],附设两个指针high, low,初始分别指向表的上界和下界 2.low<high, 从表high端依次向左搜索,找到第一个关键字小于r[0],将其移动到low处,否则继续向左移动 3.low<high, 从表low端依次向左搜索,找到第一个关键字大于r[0],将其移动到high处,否则继续向右移动 4.重复上述步骤,直到low==high,第一趟排序结束 5.递归进行排序,新枢轴分别为上一趟排序结束后枢轴左边表的第一个数和右边表的第一个数 6.当待排序的表都只有一个元素,递归结束,排序完成 |
排序的趟数取决于递归树的深度,最好为O(nlog2n),最坏情况是表已经排好序,KCN:n^2/2 改善方法:枢轴采用“三者取中” 平均为O(log2n)
|
最好:O(log2n) 最坏:O(2n) |
1.不稳定 2.不适合链表,因为需要定位上界和下界 3.适合初始值无序,n较大情况 |
| 简单选择排序 |
1.将待排序的放进数组r[1...n] 2.第一趟从r[1]开始,通过n-1次比较找出关键字中最小的记录r[k]和r[1]交换 3.第二趟从r[2]开始,通过n-2次比较找出关键字中最小的记录r[k]和r[2]交换 3.重复上述步骤 4.经过n-1趟排序完成 |
O(n^2) | 只在交换时需要一个辅助空间,所以为O(1) |
1.稳定的算法 2.适合链式存储结构 3.移动记录次数较少,当每一个记录占用空间较多,此方法比直接插入排序快 |
| 树形选择排序 | 对n个记录的关键字两两比较,在其中[n/2]个较小者之间再两两比较,重复直到选出最小关键字 | O(nlog2n) | 辅助存储空间较多,因此有了提出堆排序 | |
|
堆排 序 |
得到堆,调整堆,得到最大值,调整堆,得到最大值...重复直到最后待调整的堆只有一个元素 如何调整堆:(大根堆为例) 1.从第n-2个元素开始,直到第一个元素为止,反复筛选,若子结点大于父节点,交换两个结点的关键字 2.从上到下检查,若子结点大于父节点,交换两个结点的关键字 |
O(nlog2n) | O(1) |
1.不稳定 2.只能用于顺序结构,不能用于链式结构 3.记录少是不适合 |
|
归并 排序 |
假设初始序列n个记录,可看成n个有序的子序列,每个序列长度是1,然后 两两归并。得到n/2个长度为2或1的有序子序列,再两两归并直到得到 一个长度是n的有序序列为止 |
O(nlog2n) | O(n) |
1.稳定 2.可用于链式结构 |
对于pta作业的编程题,还是蛮有感触,当时解题一直想着用什么排序方法,没想到上学期就说过的一个投票问题其实也适用于这道题
所以说,在编程的时候,我们应该发散思维,而不是总是我们这段时间学什么就用什么的这种想法来做题,这样我们才能找到更好的解题方法
数据结构的学习已接近尾声,一学期下来,感觉还是蛮有收获的,在后期编程的学习中,希望能更好运用所学到的知识!
原文:https://www.cnblogs.com/Jacqueline--/p/13288996.html