已知实数\(a,b\)满足\(a,b\in [0,1]\),则函数\(f(x)=\frac{1}{3}x^3-ax^2+bx+c\)有极值的概率为
解答:
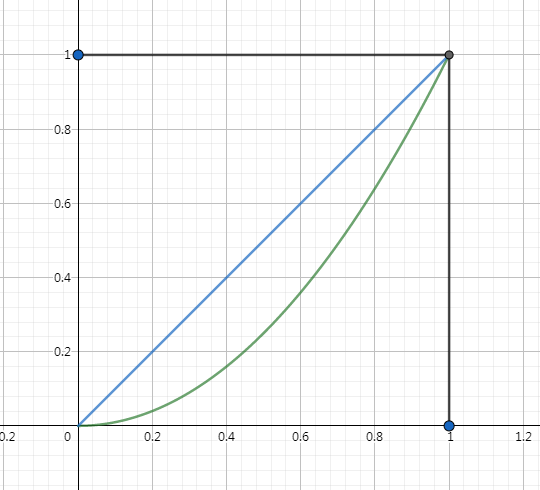
结合图像,假设我们在黑色正方形内选取任意点\((b,a)\)
\(b\)代表的值是\(y=b\)与\(y=x\)的交点,\(a\)代表的值是\(x=a\)和\(y=x^2\)的交点
显然\(y=b\)与\(y=x\)的交点在\(y=b\)上
要满足\(a^2\ge b\),应满足\(x=a\)时,\(y=x^2\)在点\((b,a)\)上方
即满足要求的点是\(y=x^2\)下方部分
对\(y=x^2\)积分得到答案为\(\frac{1}{3}\)
原文:https://www.cnblogs.com/knife-rose/p/13289678.html