题面:有一个点数为 n 的无向完全图,边权分别为 [1, n(n−1)/2 ] 之间互不相同的整数。给定该图最小生成树 上每条边的权值 ai (递增序),试求合法的无向图数量。两个无向图是不同的,当且仅当存在一条边,在 两张图中对应的端点相同而长度不同。
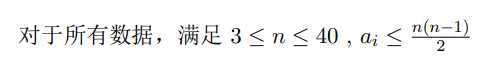
Input:
第一行包含一个整数 n。 接下来 n − 1 行,每行包含一个整数,描述了最小生成树上的一条边的权值 ai。
Output:
输出一行包含一个整数,即合法的无向图数量对 10^9 + 7 取模的结果。
这个数据范围可以让我们考虑状压。但普通的状压仅仅可能通过部分数据。我们需要优化。
我们注意到,在初始时一个n个点0条边的图如果添加n-1条边能构成一个生成树,那么每次添加边时其两侧的点必须不在同一个连通块内。因此可以考虑状态为目前图的连通块的个数和每个连通块内的点的数量。
而上面所说的状态整理一下就是一个图所有连通块大小的集合。然后开始状压。
状压的状态就是每加完一条边之后现在图所有连通块大小的集合,在n=40时最多有37338种集合,时空复杂度可以接受。
决策时从小到大来决策(所有边的边权从小到大)。我们设f[i][j]表示目前加入了第i条边后集合状态为第j种的方案数。我们假设集合状态为{n}的为第tot种,显然答案为f[m][tot]。
我们假设集合状态为{1,1,1,......,1}的为第1种,初始化时显然f[0][1]=1;
转移时有两种情况,先说第一种:第i条边在最小生成树里。
这种情况下我们仅仅连接这两个连通块就好了。注意,我们并不知道到底是哪两个连通块相连,所以我们n^2的枚举其中要相连的连通块,转移方案数。
第二种情况就是第i条边不在最小生成树里。
这意味着第i条边在某个连通块内,加入这条边后不会改变这个集合的状态。因此得到:$f[i][j]=f[i][j]+f[i-1][j]*(g[j]-(i-1));$
其中g[j]表示在状态j下有多少种添加一条边不会改变集合的状态的方案数。
对于复杂度,我们知道对于每个状态S以连接为方式的转移最多只会有1次,所以复杂度可以接受。
#include <bits/stdc++.h> #define inc(i,a,b) for(register int i=a;i<=b;i++) using namespace std; int n,m,judge[100010],tot; vector<int> now,state[100010]; map<vector<int>,int> mmap; long long g[100010]; void dfs(int rest,int pos){ if(!pos){ if(!rest){ state[++tot]=now; mmap[now]=tot; inc(j,0,(int)now.size()-1){ g[tot]+=(now[j]*(now[j]-1)/2); } } return; } dfs(rest,pos-1); if(rest>=pos){ now.push_back(pos); dfs(rest-pos,pos); now.pop_back(); } } long long f[1010][40010]; const int p=1e9+7; int main(){ freopen("tree.in","r",stdin); freopen("tree.out","w",stdout); scanf("%d",&n); m=n*(n-1)/2; inc(i,1,n-1){ int x; scanf("%d",&x); judge[x]=1; } dfs(n,n); f[0][1]=1; inc(i,1,m){ inc(j,1,tot){ if(!f[i-1][j]) continue; if(judge[i]){ long long tmp=f[i-1][j]; vector<int> ttmp=state[j]; inc(x,0,(int)ttmp.size()-1){ inc(y,x+1,(int)ttmp.size()-1){ long long tmpans=tmp*ttmp[x]%p*ttmp[y]%p; vector<int> neww; inc(z,0,(int)ttmp.size()-1){ if(z!=x&&z!=y) neww.push_back(ttmp[z]); } neww.push_back(ttmp[x]+ttmp[y]); sort(neww.begin(),neww.end()); reverse(neww.begin(),neww.end()); f[i][mmap[neww]]=(f[i][mmap[neww]]+tmpans)%p; } } } else{ f[i][j]=(f[i][j]+f[i-1][j]*(g[j]-(i-1))%p)%p; } } } cout<<f[m][tot]%p; }
原文:https://www.cnblogs.com/kamimxr/p/13289681.html