
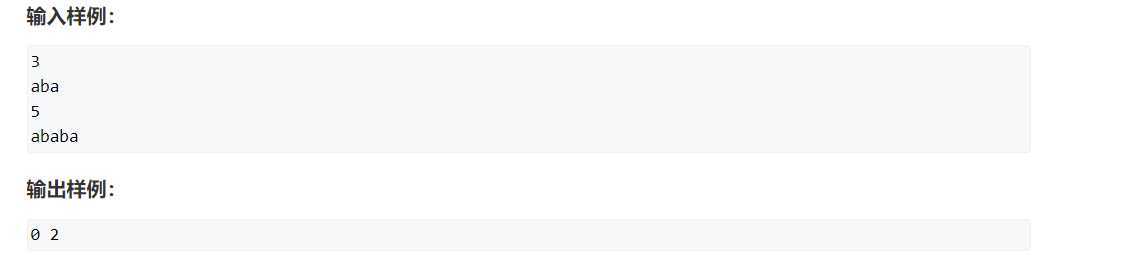
s是长串,p是子串
在数据范围较小时的暴力做法,两层循环
1 #include <bits/stdc++.h> 2 using namespace std; 3 int main() { 4 int n, m; 5 char s[100], p[100]; 6 cin >> m >> p + 1; //输入短串 7 cin >> n >> s + 1; //输入长串 8 for (int i = 1; i <= n; i++) { 9 bool flag = true; 10 for (int j = 1; j <= m; j++) { 11 if (s[i + j - 1] != p[j]) { 12 flag = false; 13 break; 14 } 15 } 16 if (flag) { 17 cout << i << " "; 18 } 19 } 20 return 0; 21 }
KMP习惯下标从1开始

KMP的核心就是在匹配失败时,p串往后最少移动到哪里继续尝试匹配
然后要实现上述操作,KMP的关键点就是:
寻找当前位置的前缀和后缀相等的长度的最大值。
为什么是最大值呢。因为这相当于每次向后移动的距离是最小的。保证不会漏掉可能的匹配起始点
也就是需要对p串的每一个点进行预处理
上面黑字这句话就是next[]数组的含义
next[i]表示以i为终点的后缀,和从1开始的前缀相等,而且这个后缀的长度最长
如果next[i] = j的话
绿颜色的长度是j
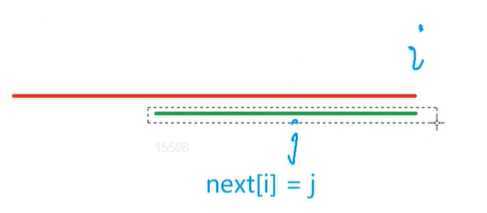
next[i] = j也就是说对于p串
p[1 ~ j] = p[i - j + 1, i]
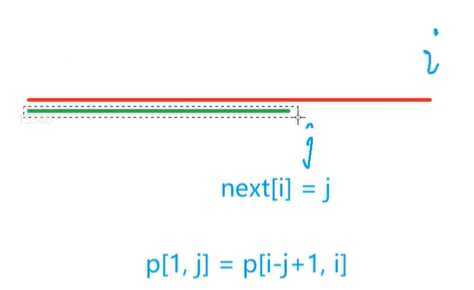
然后我们这个next数组在匹配的过程当中是如何运用的
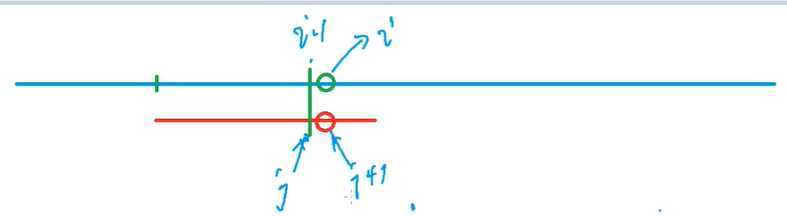
到i - 1,以及到j是匹配的
此时如果s[i] != s[j + 1]的话
然后就需要把红颜色的串,往后移动了
然后就看从前往后最少移动多少
这个最少移动多少就是直接调用next[j]
最少移动的距离就是最大的后缀
对于图中j这个点而言,也就是找到以j这个点为终点的后缀,和从1开始的前缀最长是多少
以j为终点的这一段
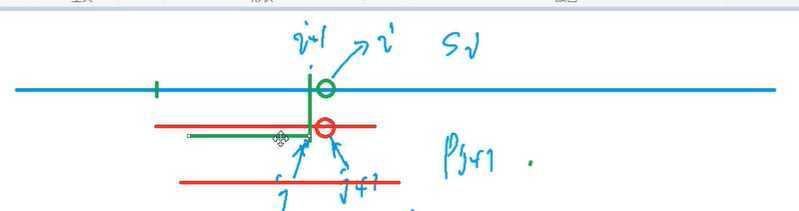
和从1开始的这一段相等
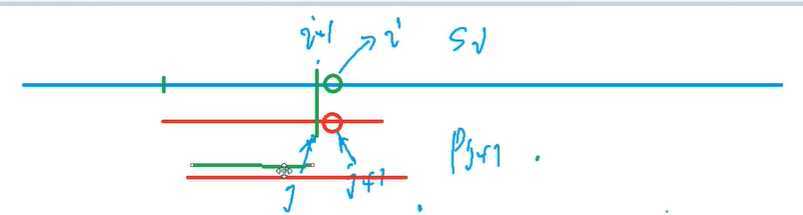
对于j这个点,直接调用next[j]
那么p串移动完之后的下标是多少,就是上图p串的绿色小串长度
也就是next[j]
也就是说p串需要移动到next[j]处
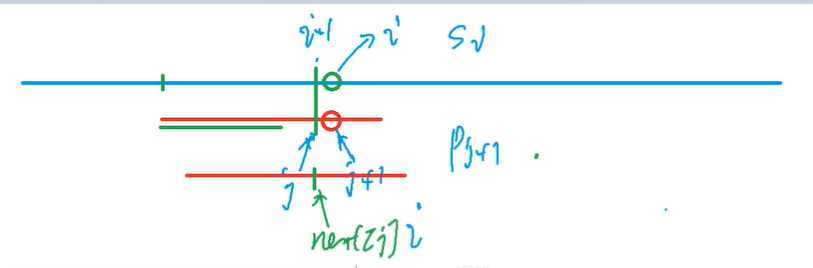
然后当我们把p串换成next[j]处之后
再看p串next[j]后的一个点是不是和s[i]匹配
如果匹配继续往后做,如果不匹配,继续调用next数组,然后再看后面一个点是否和s[i]匹配
举个样例来看p的next[]数组是啥
前缀和后缀的长度一定要小于自己的长度
ne[1] = 0 不能等于自己
ne[i]就是从1~i这一段内的,前缀和后缀相等的最大长度

时间复杂度O(n)
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 100010, M = 1000010; 4 char p[N], s[M]; //p是子串,s是原串 5 int ne[N]; //next数组,针对子串 6 int main() { 7 int n, m; 8 cin >> n >> p + 1 >> m >> s + 1; //让串的下标从1开始 9 //求next数组[]的过程 10 //1失败了就从0开始 11 for (int i = 2, j = 0; i <= n; i++) { //是对p串预处理next数组 12 while (j && p[i] != p[j + 1]) { 13 j = ne[j]; 14 } 15 if (p[i] == p[j + 1]) { 16 j++; 17 } 18 ne[i] = j; 19 } 20 //kmp的过程 21 for (int i = 1, j = 0; i <= m; i++) { //i是枚举s[i] 22 //注意当前试图和s[i]匹配的是p[j + 1] 23 while (j && s[i] != p[j + 1]) { 24 //只要j没有退回起点 25 j = ne[j]; 26 } 27 if (s[i] == p[j + 1]) { 28 j++; 29 } 30 if (j == n) { //匹配成功 31 cout << i - n << " "; //全部匹配完了,然后减去子串长度,就是起始位置 32 j = ne[j]; 33 } 34 } 35 return 0; 36 }
原文:https://www.cnblogs.com/fx1998/p/13286129.html