堆结构的概念:堆就是一个数组,它可以以完全二叉树的形式表现出来。

大根堆:完全二叉树中每棵子树的最大值都在顶部就是大根堆
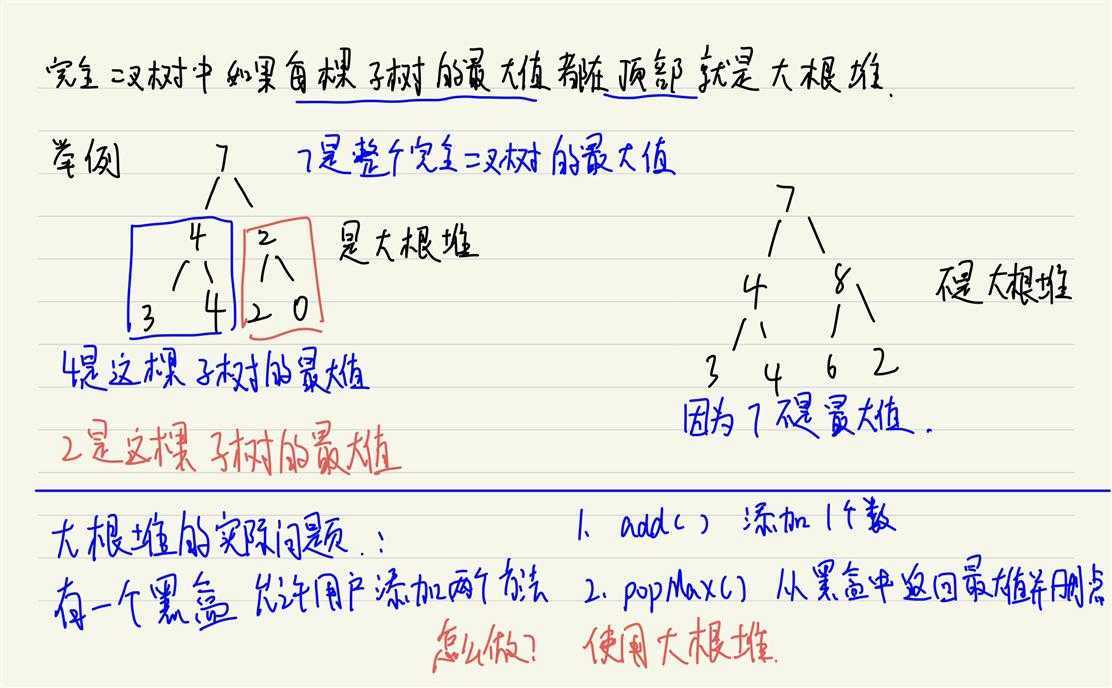
如何实现大根堆?堆操作之heapInsert

heapInsert方法来实现添加元素(一个元素一个元素的添加)

public static void heapInsert(int[] arr, int index) { //如果比父节点大,交换位置 while (arr[index] > arr[(index - 1) / 2]) { swap(arr, index, (index - 1) / 2); //继续跟父节点比较 index = (index - 1) / 2; } }
如何实现popMax操作?(找到最大值并返回,最后删掉)

堆操作之heapify方法:将一个数组调整成大根堆


/** * 方法结束后,把数组变成了新的大根堆 * <p> * 某个数处在index位置,看看能否往下沉 * 不断的和左右两个孩子进行比较 * 较大的孩子如果大于当前的父,较大孩子上来,父节点下沉。 * * @param arr:数组 * @param index:某个数处在index位置 * @param heapSize:堆的有效长度(数组的有效长度) */ public static void heapify(int[] arr, int index, int heapSize) { int left = index * 2 + 1; //父节点的左孩子的下标 while (left < heapSize) { //左孩子小于有效长度 -> 不越界 循环结束条件:左孩子超过有效长度 //largest:代表两个孩子中较大的那一个。 //判断条件:left + 1 代表右孩子,如果右孩子不越界,并且右孩子大于左孩子,要右孩子,否则要左孩子. int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ? left + 1 : left; //此时找到两个孩子中较大的一个,与父节点进行比较。谁的值大,把下标给largest largest = arr[largest] > arr[index] ? largest : index; //如果较大孩子下标 等于 父节点下标 说明不用向下沉了,结束循环 if (largest == index) { break; } //如果较大孩子的值 大于 父节点值 交换值 swap(arr, largest, index); index = largest; //把largest的下标给index left = index * 2 + 1; //继续比较 } }
通过heapInsert和heapify就可以很容易实现堆排序

public static void heapSort(int[] arr) { if (arr == null || arr.length < 2) { return; } //如果用户是一个一个的输入元素,就要使用heapInsert()方法来添加元素 for (int i = 0; i < arr.length; i++) { heapInsert(arr, i); } //如果用户一次性给了全部元素,只是用heapify方法,将全部元素(数组)构造成一个大根堆即可 //从最后一个节点开始加入 // for (int i = arr.length - 1; i >= 0; i--){ // heapify(arr,i,arr.length); // } //如何排序 ? : 将0号位置元素与最后位置元素交换,将有效长度减1 得到最后位置的元素。再变成大根堆,重复此过程 int heapSize = arr.length; swap(arr, 0, --heapSize); while (heapSize > 0) { heapify(arr, 0, heapSize); swap(arr, 0, --heapSize); } }
添加对数器后的测试结果:
原文:https://www.cnblogs.com/pxy-1999/p/13290629.html