https://www.cnblogs.com/pinard/p/6053344.html
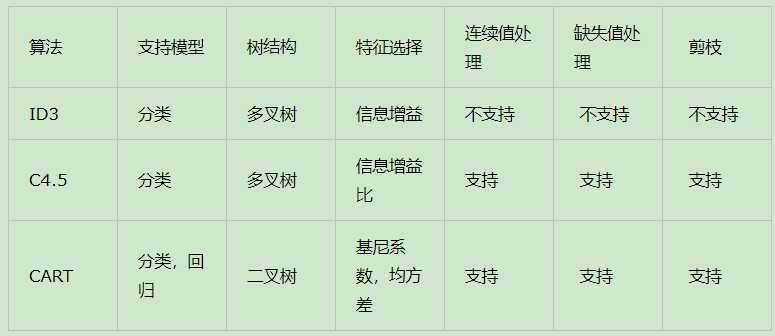
CART算法的全称是Classification And Regression Tree,采用的是Gini指数(选Gini指数最小的特征s)作为分裂标准,同时它也是包含后剪枝操作。
ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但其生成的决策树分支较大,规模较大。
为了简化决策树的规模,提高生成决策树的效率,就出现了根据GINI系数来选择测试属性的决策树算法CART。
CART分类与回归树本质上是一样的,构建过程都是逐步分割特征空间,预测过程都是从根节点开始一层一层的判断直到叶节点给出预测结果。
只不过分类树给出离散值,而回归树给出连续值(通常是叶节点包含样本的均值),
另外分类树基于Gini指数选取分割点,而回归树基于平方误差选取分割点。
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。
![]()
CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
假设有数据集 ,且
有
个分类,那么可定义基尼指数为:
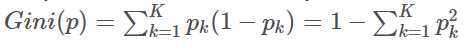
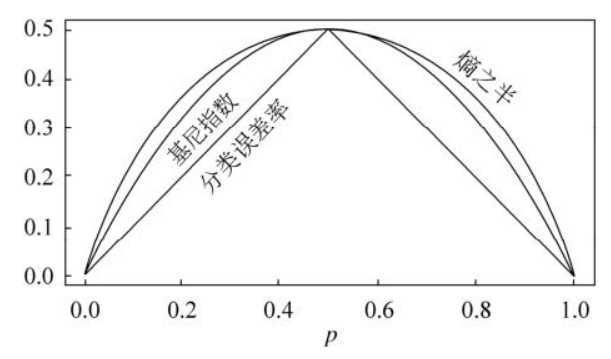
从公式可以看到,基尼指数的意义是:从数据集D中随机抽取两个样本,其类别不同的概率。直觉地,基尼指数越小,则数据集D的纯度越高。
如果训练数据集D根据特征A是否取某一可能值a被分割为D1和D2两部分,则在特征A的条件下,集合D的基尼指数定义为:
![]()
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经过A=a分割后集合D的不确定性。基尼指数越大,样本的不确定性也就越大。
相对于用信息增益/信息增益率来作为决策指标(含log操作),基尼指数的运算量比较小,也很易于理解,这是cart算法使用基尼指数的主要目的。
对于CART分类树连续值的处理问题,其思想和C4.5是相同的,都是将连续的特征离散化。
唯一的区别在于在选择划分点时的度量方式不同,C4.5使用的是信息增益比,则CART分类树使用的是基尼系数。
具体的思路如下,比如m个样本的连续特征A有m个,从小到大排列为a1,a2,...,am,则CART算法取相邻两样本值的平均数,一共取得m-1个划分点。
其中第i个划分点Ti表示为:Ti=(ai+ai+1)/2。
对于这m-1个点,分别计算以该点作为二元分类点时的基尼系数。
选择基尼系数最小的点作为该连续特征的二元离散分类点。
比如取到的基尼系数最小的点为at,则小于at的值为类别1,大于at的值为类别2,这样我们就做到了连续特征的离散化。
要注意的是,与ID3或者C4.5处理离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。
对于CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。
回忆下ID3或者C4.5,如果某个特征A被选取建立决策树节点,如果它有A1,A2,A3三种类别,我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同,他采用的是不停的二分。
还是这个例子,CART分类树会考虑把A分成{A1}和{A2,A3}, {A2}和{A1,A3}, {A3}和{A1,A2}三种情况,找到基尼系数最小的组合,比如{A2}和{A1,A3},然后建立二叉树节点,一个节点是A2对应的样本,另一个节点是{A1,A3}对应的节点。
同时,由于这次没有把特征A的取值完全分开,后面我们还有机会在子节点继续选择到特征A来划分A1和A3。这和ID3或者C4.5不同,在ID3或者C4.5的一棵子树中,离散特征只会参与一次节点的建立。


https://www.cnblogs.com/ssyfj/p/13229743.html
import numpy as np def calcGini(data_y): #根据基尼指数的定义,根据当前数据集中不同标签类出现次数,获取当前数据集D的基尼指数 m = data_y.size #获取全部数据数量 labels = np.unique(data_y) #获取所有标签值类别(去重后) gini = 1.0 #初始基尼系数 for i in labels: #遍历每一个标签值种类 y_cnt = data_y[np.where(data_y==i)].size / m #出现概率 gini -= y_cnt**2 #基尼指数 return gini
测试:
print(calcGini(np.array([1,1,2,3,2,2,1,1,3])))

def splitDataSet(data_X,data_Y,fea_axis,fea_val): #根据特征、和该特征下的特征值种类,实现切分数据集和标签 #根据伪算法可以知道,我们要将数据集划分为2部分:特征值=a和特征值不等于a eqIdx = np.where(data_X[:,fea_axis]==fea_val) neqIdx = np.where(data_X[:,fea_axis]!=fea_val) return data_X[eqIdx],data_Y[eqIdx],data_X[neqIdx],data_Y[neqIdx]
def chooseBestFeature(data_X,data_Y): #遍历所有特征和特征值,选取最优划分 m,n = data_X.shape bestFeature = -1 bestFeaVal = -1 minFeaGini = np.inf for i in range(n): #遍历所有特征 fea_cls = np.unique(data_X[:,i]) #获取该特征下的所有特征值 # print("{}---".format(fea_cls)) for j in fea_cls: #遍历所有特征值 newEqDataX,newEqDataY,newNeqDataX,newNeqDataY=splitDataSet(data_X,data_Y,i,j) #进行数据集切分 feaGini = 0 #计算基尼指数 feaGini += newEqDataY.size/m*calcGini(newEqDataY) + newNeqDataY.size/m*calcGini(newNeqDataY) if feaGini < minFeaGini: bestFeature = i bestFeaVal = j minFeaGini = feaGini return bestFeature,bestFeaVal #返回最优划分方式
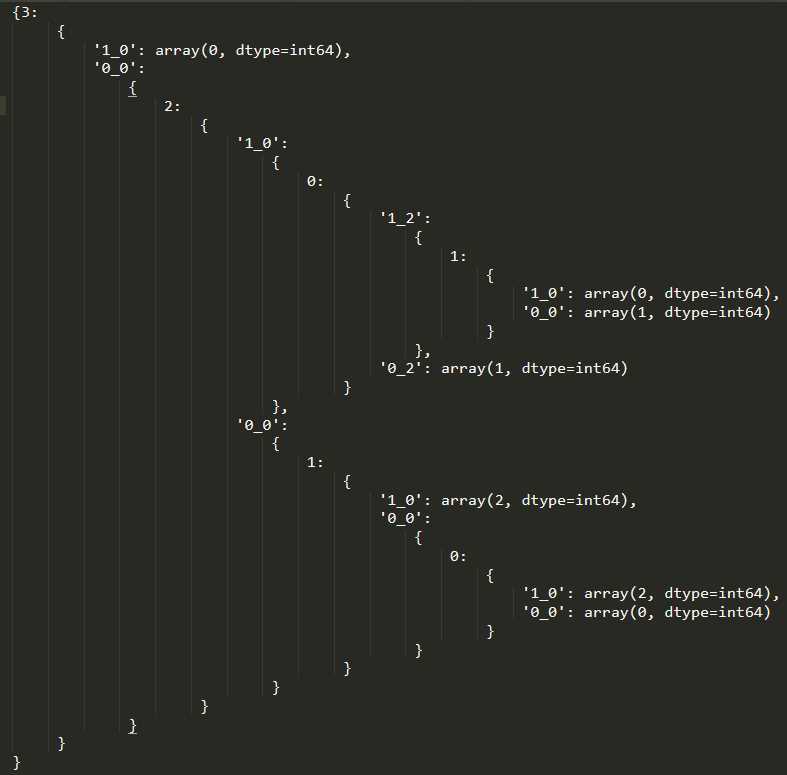
def createTree(data_X,data_Y,fea_idx): #创建决策树 y_labels = np.unique(data_Y) #1.如果数据集中,所有实例都属于同一类,则返回 if y_labels.size == 1: return data_Y[0] #2.如果特征集为空,表示遍历了所有特征,使用多数投票进行决定 if data_X.shape[1] == 0: bestFea,bestCnt = 0,0 for i in y_labels: cnt = data_Y[np.where(data_Y==i)].size if cnt > bestCnt: bestFea = i bestCnt = cnt return bestFea #按照基尼指数,选择特征,进行继续递归创建树 bestFeature, bestFeaVal = chooseBestFeature(data_X,data_Y) # print(bestFeature,bestFeaVal) feaBestIdx = fea_idx[bestFeature] my_tree = {feaBestIdx:{}} #获取划分结果 newEqDataX,newEqDataY,newNeqDataX,newNeqDataY = splitDataSet(data_X,data_Y,bestFeature,bestFeaVal) #删除我们选择的最优特征 newEqDataX = np.delete(newEqDataX,bestFeature,1) newNeqDataX = np.delete(newNeqDataX,bestFeature,1) fea_idx = np.delete(fea_idx,bestFeature,0) my_tree[feaBestIdx]["{}_{}".format(1,bestFeaVal)] = createTree(newEqDataX,newEqDataY,fea_idx) my_tree[feaBestIdx]["{}_{}".format(0,bestFeaVal)] = createTree(newNeqDataX,newNeqDataY,fea_idx) return my_tree
def preDealData(filename): df = pd.read_table(filename,‘\t‘,header = None) columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460 #数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818 new_df = pd.DataFrame() for i in range(len(columns)): new_df[i] = pd.factorize(df[i])[0] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。 data_X = new_df.values data_Y = pd.factorize(df[df.shape[1]-1])[0] #factorize返回的是ndarray类型 data_Y = np.array([data_Y]).T return data_X,data_Y,columns data_X,data_Y,fea_names = preDealData("lenses.txt")
fea_Idx = np.arange(len(fea_names)) print(createTree(data_X,data_Y,fea_Idx))

import numpy as np import pandas as pd # 创建数据集 def createDataSet(): dataSet = [[1, 1], [1, 1], [1, 0], [0, 1], [0, 1]] labels = [1, 1, 0, 0, 0] features_names = [‘水下‘, ‘脚蹼‘] # 特征名称 return dataSet, labels, features_names def calcGini(data_y): #根据基尼指数的定义,根据当前数据集中不同标签类出现次数,获取当前数据集D的基尼指数 m = data_y.size #获取全部数据数量 labels = np.unique(data_y) #获取所有标签值类别(去重后) gini = 1.0 #初始基尼系数 for i in labels: #遍历每一个标签值种类 y_cnt = data_y[np.where(data_y==i)].size / m #出现概率 gini -= y_cnt**2 #基尼指数 return gini def splitDataSet(data_X,data_Y,fea_axis,fea_val): #根据特征、和该特征下的特征值种类,实现切分数据集和标签 #根据伪算法可以知道,我们要将数据集划分为2部分:特征值=a和特征值不等于a eqIdx = np.where(data_X[:,fea_axis]==fea_val) neqIdx = np.where(data_X[:,fea_axis]!=fea_val) return data_X[eqIdx],data_Y[eqIdx],data_X[neqIdx],data_Y[neqIdx] def chooseBestFeature(data_X,data_Y): #遍历所有特征和特征值,选取最优划分 m,n = data_X.shape bestFeature = -1 bestFeaVal = -1 minFeaGini = np.inf for i in range(n): #遍历所有特征 fea_cls = np.unique(data_X[:,i]) #获取该特征下的所有特征值 # print("{}---".format(fea_cls)) for j in fea_cls: #遍历所有特征值 newEqDataX,newEqDataY,newNeqDataX,newNeqDataY=splitDataSet(data_X,data_Y,i,j) #进行数据集切分 feaGini = 0 #计算基尼指数 feaGini += newEqDataY.size/m*calcGini(newEqDataY) + newNeqDataY.size/m*calcGini(newNeqDataY) if feaGini < minFeaGini: bestFeature = i bestFeaVal = j minFeaGini = feaGini return bestFeature,bestFeaVal #返回最优划分方式 def createTree(data_X,data_Y,fea_idx): #创建决策树 y_labels = np.unique(data_Y) #1.如果数据集中,所有实例都属于同一类,则返回 if y_labels.size == 1: return data_Y[0] #2.如果特征集为空,表示遍历了所有特征,使用多数投票进行决定 if data_X.shape[1] == 0: bestFea,bestCnt = 0,0 for i in y_labels: cnt = data_Y[np.where(data_Y==i)].size if cnt > bestCnt: bestFea = i bestCnt = cnt return bestFea #按照基尼指数,选择特征,进行继续递归创建树 bestFeature, bestFeaVal = chooseBestFeature(data_X,data_Y) # print(bestFeature,bestFeaVal) feaBestIdx = fea_idx[bestFeature] my_tree = {feaBestIdx:{}} #获取划分结果 newEqDataX,newEqDataY,newNeqDataX,newNeqDataY = splitDataSet(data_X,data_Y,bestFeature,bestFeaVal) #删除我们选择的最优特征 newEqDataX = np.delete(newEqDataX,bestFeature,1) newNeqDataX = np.delete(newNeqDataX,bestFeature,1) fea_idx = np.delete(fea_idx,bestFeature,0) my_tree[feaBestIdx]["{}_{}".format(1,bestFeaVal)] = createTree(newEqDataX,newEqDataY,fea_idx) my_tree[feaBestIdx]["{}_{}".format(0,bestFeaVal)] = createTree(newNeqDataX,newNeqDataY,fea_idx) return my_tree def preDealData(filename): df = pd.read_table(filename,‘\t‘,header = None) columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460 #数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818 new_df = pd.DataFrame() for i in range(len(columns)): new_df[i] = pd.factorize(df[i])[0] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。 data_X = new_df.values data_Y = pd.factorize(df[df.shape[1]-1])[0] #factorize返回的是ndarray类型 data_Y = np.array([data_Y]).T return data_X,data_Y,columns data_X,data_Y,fea_names = preDealData("lenses.txt") print(data_X) print(data_Y) # data_x,data_y,fea_names = createDataSet() fea_Idx = np.arange(len(fea_names)) # data_X,data_Y,fea_names = createDataSet() # data_X = np.array(data_X) # data_Y = np.array(data_Y) # # fea_Idx = np.arange(len(fea_names)) print(createTree(data_X,data_Y,fea_Idx))
除了计算基尼指数,其他大多同ID3算法一致。
原文:https://www.cnblogs.com/ssyfj/p/13287016.html