嵌入模型是将知识图谱映射到向量空间的模型。正如在TransE中所提到的,用已知的三元组实体关系来构造映射,再用该映射预测未知的三元组实体关系。
自从TransE被提出以来,相继衍生了不同的变种,如TransH,TransR,TransG,pTransE。另外还有基于双线性的模型RESCAL,DistMult,HolE,ComplEx,和基于李群的TorusE。
在TransE的模型训练算法中,有三条基本原则。第一,h+r=t。第二,负抽样得到损失三元组。第三,在计算实体距离之前,对所有的实体和关系向量都进行了归一化(正则化)。这是由于向量空间可以无限扩张导致的,为了使其有界才使用了归一化,也就是在每一步计算之前将向量大小都规范到1。然而,这种规范化虽然避免了向量空间的无限扩张,但导致了新的矛盾产生。
首先从平面直观的向量和出发,在等腰三角形ΔABC中,有向量公式AB+BC=AC。假设此时||AB||=||BC||=1,且||AC||≠1,那么经过规范化后,||AB‘||=||BC’||=||AC‘||=1,在三个向量的方向不发生改变的条件下,三角形的三条边是无法闭合的。此时AB+BC≠AC,不满足第一条基本原则,即h+r=t。产生了矛盾。
其次,从向量空间的维度来看,当向量的长度被规定为某个确定的数值后,这些向量所形成的空间实际上被降维了。如在二维平面中,穷尽从原点出发的所有向量,得到的是一个圆;在三维空间中,穷尽从原点出发的所有向量,得到的是一个球面;同理适用于高维空间。当对所有n维实体向量归一化后,实际上将实体嵌入到了n-1维的向量空间中,它是n维空间的surface。若n=2,当关系也被归一化后,则可能出现以下情况:
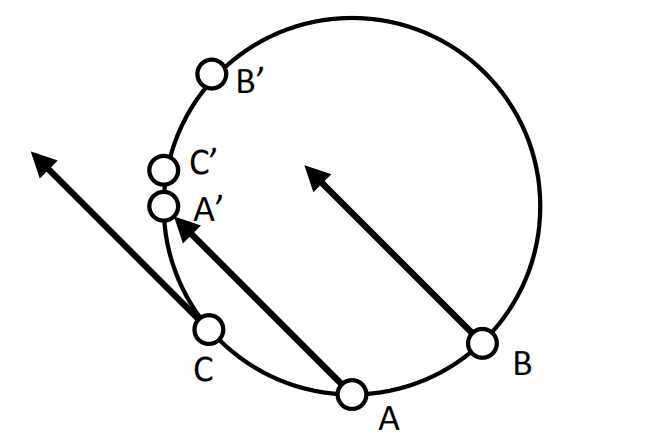
实体被映射到圆上,但已知的三元组(A,r,A‘),(B,r,B‘),(C,r,C‘)却不能很好地在图中被表示出来。这样的嵌入效果只能勉强朝h+r≈t方向努力,也会为训练带来阻碍。
TorusE就是根据TransE的局限性改进得到的,基本原则沿用了前两条。对于第三条原则,TorusE的解决方式是将映射空间由普通向量空间换成李群。
在TransE的嵌入模型中,向量空间需要满足的条件有:可微流形(局部具有欧几里得性质的空间,可以使用梯度下降法);空间中的+,-运算可微,是可交换群;可定义性,即能够定义距离函数。TorusE则在这基础之上增加了空间紧致性的条件,从而不再需要归一化。实际上,TransE中的向量空间就是一种可交换李群,但不紧致,因此用紧致的可交换李群作为嵌入空间。
李群定义:有限维光滑流形,运算的加法和逆运算都是光滑的映射,即可微、可解析的。
圆环面是一种紧致的可交换李群,呈轮胎状,如下图:
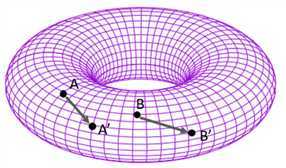
圆环面定义:一个n维圆环面Tn是一个商空间。
原文:https://www.cnblogs.com/real-zz-11/p/13291216.html