具有相同特性的数据元素的一个有限序列。
由n(n≥0)个数据元素(结点)a1,a2,...an组成的有限序列。
同一线性表中的元素必定具有相同特性,数据元素间的关系是线性关系。
开始结点
终端结点
内部结点
线性表是一种典型的线性结构
ADT List{
数据对象:D = {ai|ai属于Elemset,(i=1,2,...,n,n≥0)}
数据关系:R = {<ai-1,ai>|ai-1,ai属于D,(i=2,3,...,n)}
基本操作:
InitList(&L);
...
}ADT List
基本操作:
InitList(&L)
操作结果:构造一个空的线性表L。
DestroyList(&L)
初始条件:线性表L已经存在。
操作结果:销毁线性表L。
ClearList(&L)
初始条件:线性标L已经存在。
操作结果:将线性表L重置为空表。
ListEmpty(L)
初始条件:线性表L已经存在。
操作结果:若线性表L为空表,则返回TRUE,反之返回FALSE。
ListLength(L)
初始条件:线性表L已经存在。
操作结果:返回线性表L中的数据元素个数。
GetElem(L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)。
操作结果:用e返回线性表L中第i个数据元素的值。
LocateElem(L,e,compare())
初始条件:线性表L已经存在,compare()是数据元素判定函数。
操作结果:返回L中第1个与e满足compare()的数据元素的位序。若不存在则返回值为0。
PriorElem(L,cur_e,&pre_e)
初始条件:线性表L已经存在。
操作结果:若cur_e是L的数据元素,且不是第一个,则用pre_e返回它的前驱,反之则失败,返回NULL。
NextElem(L,cur_e,&next_e)
初始条件:线性表L已经存在。
操作结果:若cur_e是L的数据元素,且不是最后一个,则用next_e返回它的后继,反之则失败,返回NULL。
ListInsert(&L,i,e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)+1。
操作结果:在L的第i个位置之前插入新的数据元素e,L的长度加一。
ListDelete(&L,i,&e)
初始条件:线性表L已经存在,1≤i≤ListLength(L)。
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减一。
ListTraverse(&L,visited())
初始条件:线性表L已经存在。
操作结果:依次对线性表中每个元素调用visited()。
可以根据公式计算出任何一个数据元素的存储地址,所以访问每个元素所花时间相等。
模板
#define LIST_INIT_SIZE 100 //线性表存储空间的初始分配量
typedef struct{
ElemType elem[LIST_INIT_SIZE];
int length;
}SqList;
例子
多项式
#define MAXSIZE 1000
typedef struct{ //多项式定义
float p; //系数
int e; //指数
}Polynomial;
typedef struct{
Polynomial *elem; //存储空间的基地址
int length; //多项式中当前项的个数
}SqList;
void main(){
Polynomial a[MAXSIZE];
int i;
for(i=0;i<MAXSIZE;i++){
Polynomial temp;
char msg;
printf("输入系数:");
scanf("%f",&temp.p);
printf("输入指数:");
scanf("%d",&temp.e);
a[i] = temp;
printf("是否退出(y):\n");
msg = getch();
if(msg == ‘y‘){
break;
}
}
SqList b;
b.elem = a;
b.length = i+1;
for(i=0;i<b.length;i++){
Polynomial temp;
temp = b.elem[i];
if(temp.e == 0){
printf("%0.2f +",temp.p);
}else if(temp.e == 1){
printf("%0.2fx +",temp.p);
}else{
printf("%0.2fx^%d +",temp.p,temp.e);
}
}
}
为确定记录在表中的位置,需要与给定值进行比较的关键字的个数的期望值叫做查找算法的平均查找长度。
顺序查找的平均查找长度:
插入位置在最后:不需要移动任何元素
插入位置在中间:移动元素的个数与插入的位置有关
插入位置在最前面:需要移动所有元素
删除位置在最后:不需要移动任何元素
删除位置在中间:移动元素的个数与删除的位置有关
删除位置在最前面:需要移动所有元素
结点:数据元素的存储映像。由数据域和指针域组成
链表:n个结点由指针链组成一个链表。
单链表、双链表、循环链表、双向循环链表。



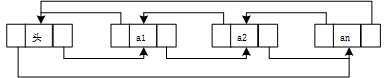
头指针、头结点和首元结点

访问每个数据元素的时间与所处位置有关。
模板
typedef struct Lnode{
ElemType data; //数据域
struct Lnode *next; //指针域
}Lnode,*LinkList; //Lnode为这个结构体的类型,*LinkList为指向这个结构体的指针类型
例如
多项式
typedef struct{
int zhishu;
float xishu;
}ElemType;
typedef struct Lnode{
ElemType data;
struct Lnode *next;
}Lnode,*LinkList;
Lnode * InitList(){
Lnode *L = (Lnode *) malloc(sizeof(Lnode));
if (L == NULL){
exit(0);
}
L->data = 10;
L->next = NULL;
return L;
}
int IsEmpty(Lnode *L){
if(L->next){
return 1;
}else{
return 0;
}
}
void DestroyList(Lnode *L){
Lnode *p;
while(L){
p = L;
L = L->next;
free(p);
p->next = NULL;
}
}
void ClearList(Lnode *L){
Lnode *p,*q;
p = L->next;
while(p){
q = p->next;
free(p);
p = q;
}
L->next = NULL;
}
int ListLength(Lnode *L){
Lnode *p;
int length = 0;
p = L->next;
while (p){
p = p->next;
length++;
}
return length;
}
ElemType GetElem(Lnode *L,int index){
Lnode *p = L->next;
int temp = 1;
while (p && temp < index){
p = p->next;
temp++;
}
if (p && temp == index){
return p->data;
}
}
Lnode * LocateElem(Lnode *L,ElemType data){
Lnode *p = L->next;
while (p){
if (p->data.xishu == data.xishu && p->data.zhishu == data.zhishu){
break;
}
p = p->next;
}
return p;
}
int ListInsert(Lnode *L,int index,ElemType data){
Lnode *p = L;
int temp = 0;
while (p && temp<index-1){
p = p->next;
temp++;
}
if (p && temp == index){
Lnode *s = (Lnode *)malloc(sizeof(Lnode));
s->data = data;
s->next = p->next;
p->next = s;
return 1;
}
return 0;
}
int DeleteList(Lnode *L,int index){
Lnode *p = L;
int temp = 0;
while (p && temp<index-1){
p = p->next;
temp++;
}
if (p && temp==index-1){
Lnode *s = p->next;
p->next = s->next;
free(s);
}
}
void ListInsert_Head(Lnode *L,ElemType data[]){
//此代码用CLion测试过,其实sizeof(data)应该为(sizeof(data)/sizeof(ElemType))-1,不知道为什么CLion自动计算长度了。
for (int i = sizeof(data); i > -1 ; --i) {
Lnode *s = (Lnode *)malloc(sizeof(Lnode));
s->data = data[i];
s->next = L->next;
L->next = s;
}
}
void ListInsert_Last(Lnode *L,ElemType data[]){
Lnode *p = L;
//此代码用CLion测试过,其实sizeof(data)应该为(sizeof(data)/sizeof(ElemType))-1,不知道为什么CLion自动计算长度了。
for (int i = 0; i <= sizeof(data) ; ++i) {
Lnode *s = (Lnode *)malloc(sizeof(Lnode));
s->data = data[i];
s->next = NULL;
p->next = s;
p = s;
}
}
时间效率分析
查找
线性链表只能顺序存取,只能从头指针开始找,查找时间复杂度为O(n)。
插入和删除
插入和删除只需要修改指针,所以时间复杂度为O(1),如需删除指定位置的结点,就需要从头查找其指定位置的前驱结点,所以时间复杂度为O(n)。
由于表的操作通常是在表的首尾进行操作,而链表的头指针表示的查找第一个的时间复杂度为O(1)、查找最后一个的时间复杂度为O(n),因此引入尾指针,尾指针表示的查找第一个的时间复杂度为O(1)、查找最后一个的时间复杂度为O(1)。
尾指针
最后一个结点的指向头结点。
Lnode * ChangeList(Lnode *L){
Lnode *p = L;
while (L){
if (L->next == NULL){
L->next = p;
break;
}
L = L->next;
}
return L;
}
Lnode * AddCirculationList(Lnode *L,ElemType data){
Lnode *p = L;
Lnode *s = (Lnode *)malloc(sizeof(Lnode));
s->data = data;
s->next = L->next;
L->next = s;
return s;
}
Lnode * MergeList(Lnode *L,Lnode *P){
Lnode *l = L->next;
L->next = P->next->next;
free(P->next);
P->next = l;
return P;
}
在单链表的每个结点中增加一个指向其直接前驱的指针域prior。
LnodeDul * GetElemDul(LnodeDul *L,int index){
LnodeDul *p = L;
int temp = 0;
while (p && temp<index){
p = p->next;
temp++;
}
if (p && temp == index){
return p;
}
}
int ListInsertDul(Lnode *L,int index,ElemType data){
LnodeDul *p;
if (!(p = GetElemDul(L,index))){
return 0;
}
LnodeDul *s = (LnodeDul *)malloc(sizeof(LnodeDul));
s->data = data;
s->prior = p->prior;
p->prior->next = s;
s->next = p;
p->prior = s;
return 1;
}
int ListDeleteDul(LnodeDul *L,int index){
LnodeDul *p;
if (!(p=GetElemDul(L,index))){
return 0;
}
p->prior->next = p->next;
p->next->prior = p->prior;
free(p);
return 1;
}
| 带头结点 | 找头结点 | 找尾结点 | 找当前结点p的前驱结点 |
|---|---|---|---|
| 单链表(头指针L) | L->next 时间复杂度O(1) | 从头遍历 时间复杂度O(n) | 无法找到 |
| 循环链表(头指针L) | L->next 时间复杂度O(1) | 从头遍历 时间复杂度O(n) | 从P->next遍历 时间复杂度O(n) |
| 循环链表(尾指针R) | R->next 时间复杂度O(1) | R本身 时间复杂度O(1) | 从P->next遍历 时间复杂度O(n) |
| 双向循环链表(头指针L) | L->next 时间复杂度O(1) | L->prior 时间复杂度O(1) | p->prior 时间复杂度O(1) |
不需要一段连续的内存空间;
结点空间可以动态申请和释放;
插入和删除时不需要移动数据元素,只需要改变结点的指针域即可。
存储密度越大,存储空间利用率越高。顺序表存储密度为1,链表存储密度小于1。
List union(List La,List Lb){
//获取长度
La_len = ListLength(La);
Lb_len = ListLength(Lb);
//把Lb中每一个元素在La中查找,没找到,则添加;反之,则跳过。
for(int i = 1;i<=Lb_len;i++){
ElemType e = GetElem(Lb,i);
if(!LocatElem(La,e)){
ListInsert(La,++La_len,e);
}
}
}
时间复杂度为:O(ListLength(La)*ListLength(Lb))
空间复杂度为:O(1)
SqList MergeList(SqList La,SqList Lb){
Polynomial *pa = La.elem;
Polynomial *pb = Lb.elem;
SqList pc;
pc.length = La.length+Lb.length;
pc.elem = Polynomial[pc.length];
Polynomial pc[] = pc.elem;
pa_end = La.elem+La.length-1;
pb_end = Lb.elem+Lb.length-1;
while(pa<=pa_end && pb<=pb_end){
if(*pa <= *pb){
*pc++ = *pa++;
}else{
*pc++ = *pb++;
}
}
while(pa <= pa_end){
*pc++ = *pa++;
}
while(pb <= pb_end){
*pc++ = *pb++;
}
return pc;
}
时间复杂度为:O(La.length+Lb.length)
空间复杂度为:O(La.length+Lb.length)
void ListUnion(Lnode *La,Lnode *Lb){
Lnode *La_fast = La->next;
Lnode *Lb_fast = Lb->next;
Lnode *p = La;
while (La_fast && Lb_fast){
if (La_fast->data <= Lb_fast->data){
p->next = La_fast;
p = La_fast;
La_fast = La_fast->next;
} else{
p->next = Lb_fast;
p = Lb_fast;
Lb_fast = Lb_fast->next;
}
}
p->next = La_fast ? La_fast : Lb_fast;
free(Lb);
}
时间复杂度为:O(min(La,Lb))
空间复杂度为:O(1)
固定版
#include <stdio.h>
int main()
{
float Pa[] = {10,5,-4,3,2,0,0,0,0,5};
float Pb[] = {-3,8,4,0,-5,7,-2,0,0,7};
float Pc[] = {0,0,0,0,0,0,0,0,0,0};
for (int i = 0; i < 9; ++i) {
Pc[i] = Pa[i]+Pb[i];
}
Pc[9] = Pa[9]<Pb[9] ? Pb[9] : Pa[9];
for (int j = 0; j < Pc[9]; ++j) {
if (j == Pc[9]-1){
printf("%0.1fX^%d",Pc[j],j);
} else {
printf("%0.1fX^%d+",Pc[j],j);
}
}
return 0;
}
自定义版
#include <stdio.h>
#define PolynomialMax 20
int main()
{
float Pa[PolynomialMax],Pb[PolynomialMax];
for (int m = 0; m < PolynomialMax; ++m) Pa[m] = Pb[m] = 0;
for (int i = 1; i < 3; ++i) {
int q = 0;
printf("多项式:%d\n", i);
while (1) {
float temp;
printf("输入指数为%d的系数:", q);
scanf("%f", &temp);
if (i == 1) {
Pa[q] = temp;
Pa[PolynomialMax - 1] = q + 1;
} else {
Pb[q] = temp;
Pb[PolynomialMax - 1] = q + 1;
}
fflush(stdin);
q++;
printf("是否结束(Y/N)");
char quit;
scanf("%c", &quit);
if (quit == ‘Y‘ || q == PolynomialMax - 1) break;
}
}
for (int j = 0; j < 2; ++j) {
for (int k = 0; k < PolynomialMax; ++k) {
if (j==0){
if (k == Pa[PolynomialMax-1]-1){
printf("%0.2fX^%d",Pa[k],k);
printf("\n");
break;
} else {
printf("%0.2fX^%d+",Pa[k],k);
}
} else {
if (k == Pa[PolynomialMax-1]-1){
printf("%0.2fX^%d",Pb[k],k);
printf("\n");
break;
} else {
printf("%0.2fX^%d+",Pb[k],k);
}
}
}
}
float Pc[PolynomialMax];
for (int n = 0; n < PolynomialMax; ++n) Pc[n] = 0;
Pc[PolynomialMax-1] = Pa[PolynomialMax-1] < Pb[PolynomialMax-1] ? Pb[PolynomialMax-1] : Pa[PolynomialMax-1];
for (int l = 0; l < Pc[PolynomialMax-1]; ++l) Pc[l] = Pa[l]+Pb[l];
for (int i1 = 0; i1 < Pc[PolynomialMax-1]; ++i1) printf("%0.2fX^%d+",Pc[i1],i1);
return 0;
}
SparsePolynomial.h
//
// Created by admin on 2020/7/12.
//
#include <stdio.h>
#include <stdlib.h>
#ifndef DATASTRUCTURE_SPARSEPOLYNOMIAL_H
#define DATASTRUCTURE_SPARSEPOLYNOMIAL_H
#define MAXELEMLENGTH 20
typedef struct {
int index;
float coefficient;
}Polynomial;
typedef struct{
Polynomial *elem;
int length;
}SqList;
typedef struct LNode{
Polynomial date;
struct LNode *prior;
struct LNode *next;
}LNode,*LinkList;
//创建线性表
SqList CreateSqList();
//添加项
int AddPolynomialSqList(SqList *L,Polynomial data);
//多项式相加
SqList UnionSqList(SqList *L,SqList *Q);
//创建双向链表
LinkList CreateLNode();
//添加结点
LinkList AddPolynomialLNode(LinkList L,Polynomial data);
//多项式相加
LinkList UnionLNode(LinkList L,LinkList p);
#endif //DATASTRUCTURE_SPARSEPOLYNOMIAL_H
SParsePolunomial.c
//
// Created by admin on 2020/7/12.
//
#include "SparsePolynomial.h"
SqList CreateSqList(){
Polynomial *polynomialList = (Polynomial *)malloc(sizeof(Polynomial) * MAXELEMLENGTH);
if (polynomialList == NULL){
exit(0);
}
SqList sqList;
sqList.elem = polynomialList;
sqList.length = 0;
return sqList;
}
int AddPolynomialSqList(SqList *L,Polynomial data){
if (L->length >= MAXELEMLENGTH){
return 0;
}
L->elem[L->length] = data;
L->length++;
return 1;
}
SqList UnionSqList(SqList *L,SqList *Q){
int LStart,QStart;
LStart = QStart = 0;
Polynomial *polynomialList = (Polynomial *)malloc(sizeof(Polynomial) * (L->length+Q->length));
if (polynomialList == NULL){
exit(0);
}
SqList sqList;
sqList.elem = polynomialList;
sqList.length = 0;
while (LStart < L->length && QStart < Q->length){
if (L->elem[LStart].index == Q->elem[QStart].index){
Polynomial polynomial;
polynomial.index = L->elem[LStart].index;
polynomial.coefficient = L->elem[LStart++].coefficient + Q->elem[QStart++].coefficient;
if (polynomial.coefficient != 0) {
sqList.elem[sqList.length++] = polynomial;
}
} else if (L->elem[LStart].index < Q->elem[QStart].index){
sqList.elem[sqList.length++] = L->elem[LStart++];
} else if (L->elem[LStart].index > Q->elem[QStart].index){
sqList.elem[sqList.length++] = Q->elem[QStart++];
}
}
while (LStart < L->length){
sqList.elem[sqList.length++] = L->elem[LStart++];
}
while (QStart < Q->length){
sqList.elem[sqList.length++] = Q->elem[QStart++];
}
return sqList;
}
LinkList CreateLNode(){
LinkList linkList = (LinkList)malloc(sizeof(LNode));
if (linkList == NULL){
exit(0);
}
linkList->prior = NULL;
linkList->next = linkList;
return linkList;
}
LinkList AddPolynomialLNode(LinkList L,Polynomial data){
LinkList linkList = CreateLNode();
linkList->date = data;
linkList->prior = L;
linkList->next = L->next;
linkList->next->prior = linkList;
L->next = linkList;
return linkList;
}
LinkList UnionLNode(LinkList L,LinkList P){
LinkList SL = L->next->next;
LinkList SP = P->next->next;
LinkList SS = CreateLNode();
while (1){
if (SL->date.index == SP->date.index){
Polynomial polynomial;
polynomial.index = SL->date.index;
polynomial.coefficient = SL->date.coefficient + SP->date.coefficient;
if (polynomial.coefficient != 0){
SS = AddPolynomialLNode(SS,polynomial);
}
SL = SL->next;
SP = SP->next;
} else if (SL->date.index < SP->date.index){
SS = AddPolynomialLNode(SS,SL->date);
SL = SL->next;
} else if (SL->date.index > SP->date.index){
SS = AddPolynomialLNode(SS,SP->date);
SP = SP->next;
}
if (SL == L->next || SP == P->next){
break;
}
}
while (SL != L->next){
SS = AddPolynomialLNode(SS,SL->date);
SL = SL->next;
}
while (SP != P->next){
SS = AddPolynomialLNode(SS,SP->date);
SP = SP->next;
}
return SS;
}
main.c
#include <stdio.h>
#include "SparsePolynomial.h"
int main()
{
int indexL[] = {0,1,2,3,4};
int indexQ[] = {0,1,2,4,5,6};
float coefficientL[] = {10,5,-4,3,2};
float coefficientQ[] = {-3,8,4,-5,7,-2};
Polynomial polynomial;
printf("稀疏多项式线性表顺序表实现相加:");
SqList sqListL;
SqList sqListQ;
sqListL = CreateSqList();
sqListQ = CreateSqList();
for (int i = 0; i < sizeof(indexL)/sizeof(int); ++i) {
polynomial.index = indexL[i];
polynomial.coefficient = coefficientL[i];
AddPolynomialSqList(&sqListL,polynomial);
}
for (int j = 0; j < sizeof(indexQ)/sizeof(int); ++j) {
polynomial.index = indexQ[j];
polynomial.coefficient = coefficientQ[j];
AddPolynomialSqList(&sqListQ,polynomial);
}
SqList sqList;
sqList = UnionSqList(&sqListL,&sqListQ);
for (int k = 0; k < sqList.length; ++k) {
if (k == sqList.length-1){
printf("%.0f*X^%d",sqList.elem[k].coefficient,sqList.elem[k].index);
} else{
printf("%.0f*X^%d+",sqList.elem[k].coefficient,sqList.elem[k].index);
}
}
printf("\n");
printf("稀疏多项式线性表双向链表(尾指针)实现相加:");
LinkList linkListL,linkListQ;
linkListL = CreateLNode();
linkListQ = CreateLNode();
for (int i = 0; i < sizeof(indexL)/sizeof(int); ++i) {
polynomial.index = indexL[i];
polynomial.coefficient = coefficientL[i];
linkListL = AddPolynomialLNode(linkListL,polynomial);
}
for (int j = 0; j < sizeof(indexQ)/sizeof(int); ++j) {
polynomial.index = indexQ[j];
polynomial.coefficient = coefficientQ[j];
linkListQ = AddPolynomialLNode(linkListQ,polynomial);
}
LinkList linkList;
linkList = UnionLNode(linkListL,linkListQ);
LinkList temp = linkList->next->next;
while (1){
if (temp == linkList){
printf("%.0f*X^%d",temp->date.coefficient,temp->date.index);
}
else{
printf("%.0f*X^%d+",temp->date.coefficient,temp->date.index);
}
temp = temp->next;
if (temp == linkList->next){
break;
}
}
return 0;
}
顺序表与链表
LibraySystem.h
//
// Created by admin on 2020/7/12.
//
#include <stdio.h>
#include <stdlib.h>
#ifndef DATASTRUCTURE_LIBRARYSYSTEM_H
#define DATASTRUCTURE_LIBRARYSYSTEM_H
#define MAXBOOKSNUMBER 100
typedef struct {
char id[20];
char name[50];
float price;
}Book;
typedef struct {
Book *elem;
int length;
}SqList;
typedef struct LNode{
Book date;
struct LNode *prior;
struct LNode *next;
}LNode,*LinkList;
//创建线性表
SqList CreateSqList();
//添加项
int AddPolynomialSqList(SqList *L,Book data);
//多项式相加
SqList UnionSqList(SqList *L,SqList *Q);
//创建双向链表
LinkList CreateLNode();
//添加结点
LinkList AddPolynomialLNode(LinkList L,Book data);
//多项式相加
LinkList UnionLNode(LinkList L,LinkList p);
#endif //DATASTRUCTURE_LIBRARYSYSTEM_H
LibraySystem.c
//
// Created by admin on 2020/7/12.
//
#include "LibrarySystem.h"
SqList CreateSqList(){
Book *book = (Book *)malloc(sizeof(Book) * MAXBOOKSNUMBER);
if (book == NULL){
exit(0);
}
SqList sqList;
sqList.elem = book;
sqList.length = 0;
return sqList;
}
int AddPolynomialSqList(SqList *L,Book data){
if (L->length >= MAXBOOKSNUMBER){
return 0;
}
L->elem[L->length] = data;
L->length++;
return 1;
}
LinkList CreateLNode(){
LinkList linkList = (LinkList)malloc(sizeof(LNode));
if (linkList == NULL){
exit(0);
}
linkList->prior = NULL;
linkList->next = linkList;
return linkList;
}
LinkList AddPolynomialLNode(LinkList L,Book data){
LinkList linkList = CreateLNode();
linkList->date = data;
linkList->prior = L;
linkList->next = L->next;
linkList->next->prior = linkList;
L->next = linkList;
return linkList;
}
main.c
#include <stdio.h>
#include <string.h>
#include "LibrarySystem.h"
int main()
{
SqList sqList;
sqList = CreateSqList();
char ISBN[5][20] = {"9787302257642","9787302257643","9787302257644",
"9787302257654","9787302257656"};
char Name[5][50] = {"数据库原理","计算机网络","数据结构","编译原理","计算机组成原理"};
float Price[5] = {25,35.5,45,78.5,99};
for (int i = 0; i < 5; ++i) {
Book book;
strcpy(book.id,ISBN[i]);
strcpy(book.name,Name[i]);
book.price = Price[i];
AddPolynomialSqList(&sqList,book);
}
LinkList linkList;
linkList = CreateLNode();
for (int j = 0; j < sqList.length; ++j) {
printf("%s\t%s\t%.2f\n",sqList.elem[j].id,sqList.elem[j].name,sqList.elem[j].price);
linkList = AddPolynomialLNode(linkList,sqList.elem[j]);
}
LinkList temp = linkList->next->next;
while (1){
printf("%s\t%s\t%.2f\n",temp->date.id,temp->date.name,temp->date.price);
temp = temp->next;
if (temp == linkList->next){
break;
}
}
return 0;
}
原文:https://www.cnblogs.com/lisztomania/p/13301895.html