题:https://ac.nowcoder.com/acm/contest/5667/I
题意:最初的区间为[1,n],给定可供选择且有代价的区间变换限制,求最小代价选择让初始区间不变为l==r或输出-1表示不能达到
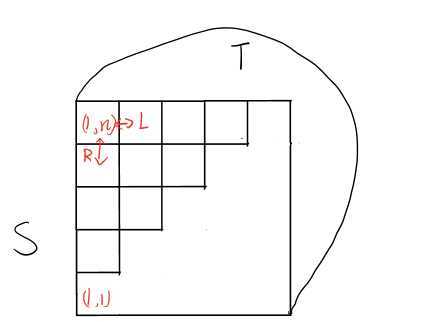
分析: 把[l,r]区间转化为网格图上的(l,r),区间变化则为网格图上边的容量;
将其转化为对偶图求最短路即可,对应建图大概如下:

#include<bits/stdc++.h> using namespace std; typedef long long ll; #define pb push_back const int M=5e5+5;; const int inf=0x3f3f3f3f; const ll INF=1e18; ll dis[M]; bool vis[M]; int id[505][505]; struct node{ int v; ll c; node(int V=0,ll C=0):v(V),c(C){} bool operator <(const node &b)const { return c>b.c; } }; struct Edge{ int v; ll cost; Edge(int V=0,ll Cost=0):v(V),cost(Cost){} }; vector<Edge>g[M]; void addedge(int u,int v,ll w){ g[u].push_back(Edge(v,w)); g[v].push_back(Edge(u,w)); } void dij(int st,int n){ priority_queue<node>que; for(int i=1;i<=n;i++) dis[i]=INF; while(!que.empty())que.pop(); dis[st]=0; que.push(node(st,0)); while(!que.empty()){ node tmp=que.top(); que.pop(); int u=tmp.v; if(vis[u]) continue; vis[u]=true; for(auto it:g[u]){ int v=it.v; ll cost=it.cost; if(!vis[v]&&dis[v]>dis[u]+cost){ dis[v]=dis[u]+cost; que.push(node(v,dis[v])); } } } } int main(){ int n,m,tot=0; scanf("%d%d",&n,&m); for(int i=1;i<=n-1;i++) for(int j=i;j<=n-1;j++) id[i][j]=++tot; int s=++tot,t=++tot; for(int i=1;i<=m;i++){ int l,r; ll w; char op[2]; scanf("%d%d%s%lld",&l,&r,op,&w); if(op[0]==‘L‘){ if(r==n) addedge(id[l][r-1],t,w); else addedge(id[l][r],id[l][r-1],w); } else{ if(l==1) addedge(id[l][r-1],s,w); else addedge(id[l][r-1],id[l-1][r-1],w); } } dij(s,t); if(dis[t]>=INF) puts("-1"); else printf("%lld\n",dis[t]); return 0; }
原文:https://www.cnblogs.com/starve/p/13311187.html