快速排序

交换排序：

1. 冒泡排序
2. 快速排序

算法思想：

先找一个基准元素，比它小的往左去，比它大的往右去。

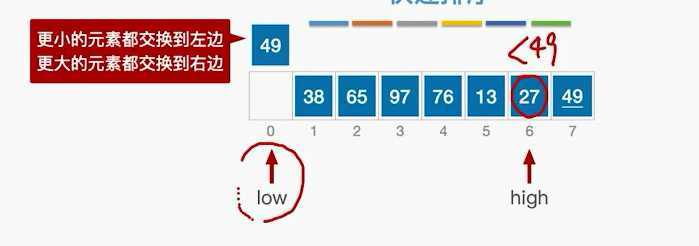
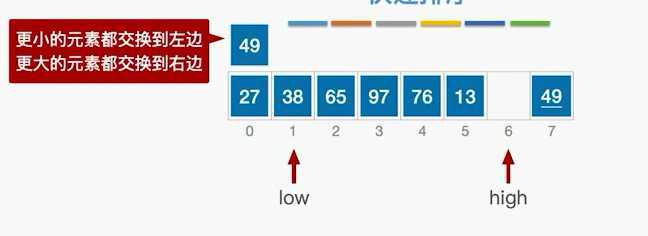
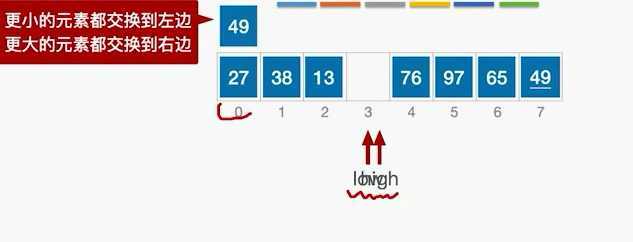
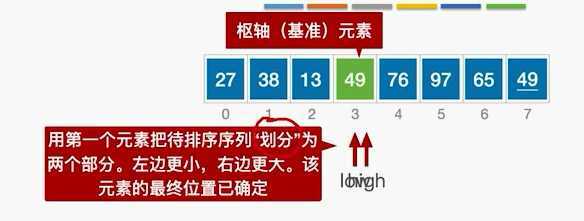
分成左右两块重复操作。

不断划分，左边都小于基准元素，右边都大于基准元素。

代码（非常重要！！！）

//用第一个元素将待排序序列划分成左右两个部分
int Partition(int A[],int low,int high){
    int pivot=A[low];		//第一个元素作为枢纽
    while(low<high){		//用low、high搜索枢纽的最终位置
        while(low<high&&A[high]>=pivot) --high;
        A[low]=A[high];		//比枢纽小的元素移动到左端
        while(low<high&&A[low]<=pivot) ++low;
        A[high]=A[low];		//比枢纽大的元素移动到右端
    }
    A[low]=pivot;			//枢纽元素存放到最终位置
    return low;				//返回存放枢纽的最终位置
}

//快速排序
void QuickSort(int A[],int low,int high){
    if(low<high){		//边界条件
        int pivotpos=Partition(A,low,high);
        QuickSort(A,low,pivotpos-1);
        QuickSort(A,pivotpos+1,high);
    }
}

算法效率分析

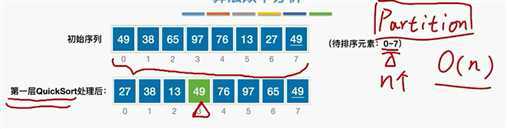
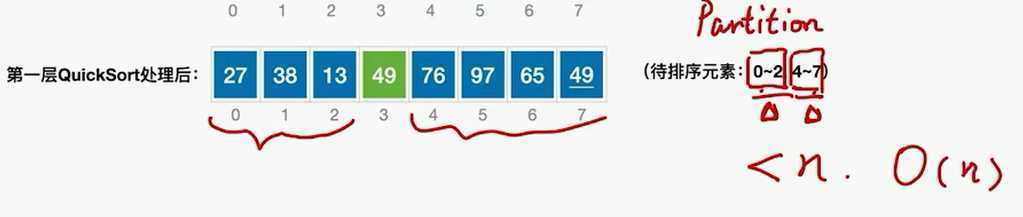
每一层的QuickSork只需要处理剩余待排序元素，时间复杂度不会超过O(n)

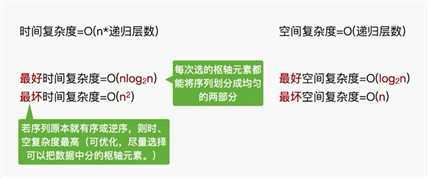
时间复杂度=O(n*递归层数)

空间复杂度=O(递归层数)

递归工作栈。

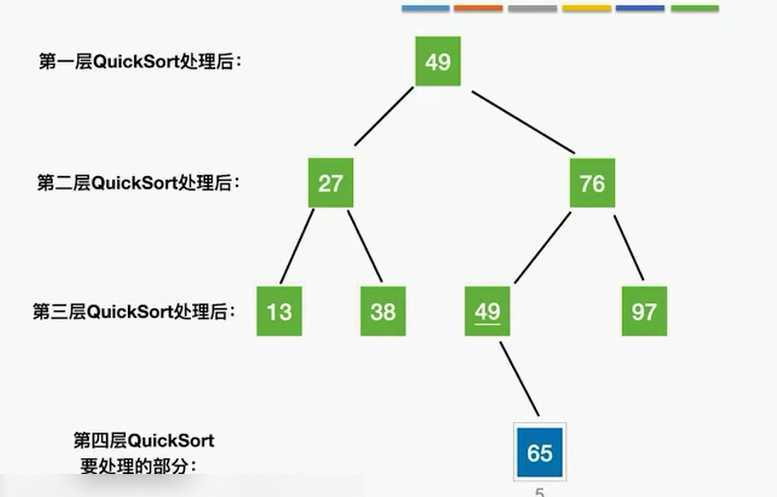
把n个元素组织成二叉树，二叉树的层数就是递归调用的层数

n个结点的二叉树，最小高度=log2n向下取整+1

最大高度=n

比较好的情况

每一次选中”枢轴“将待排序序列划分为均匀的两个部分，则递归深度最小，算法效率最高

最坏的情况

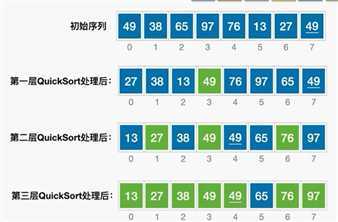
每一次选中的”枢轴“将待排序序列划分为很不均匀的两个部分，则会导致递归深度增加，算法效率变低。

若初始序列有序或逆序，则快速排序的性能最差（因为每次选择的都是最靠边的元素）

快速排序算法优化思路

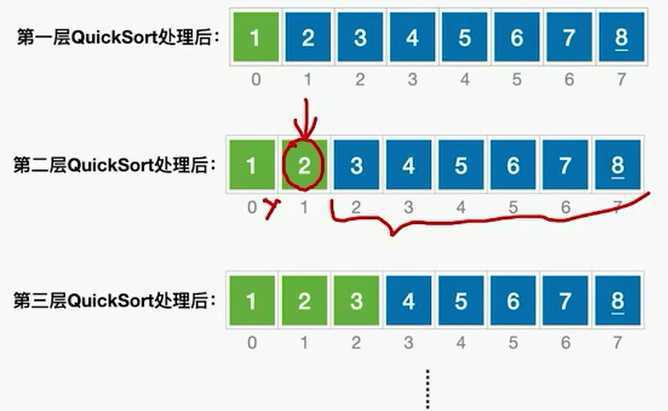
尽量选择可以把数据中分的枢轴元素。

1. 选头、中、尾三个位置的元素，取中间值作为枢轴元素；
2. 随机选一个元素作为枢轴元素

稳定性

不稳定

知识回顾

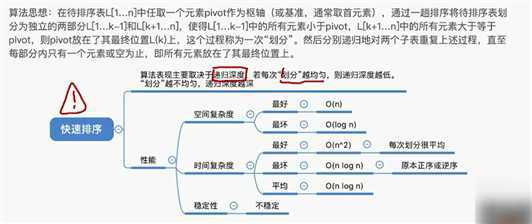
代码需要能够完完全全手写出来。

快速排序

原文：https://www.cnblogs.com/jev-0987/p/13322161.html