插入排序

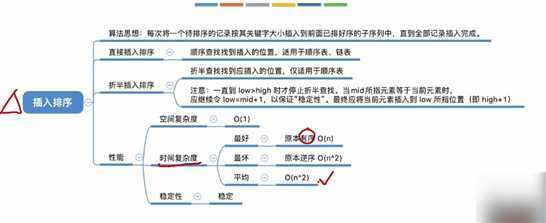
每次将一个待排序的记录按其关键字大小插入到前面已经排好序的子序列中，直到全部记录插入完成

算法实现

//直接插入排序
void InsertSort(int A[] , int n){
    int i,j,temp;
    for(i=1;i<n;i++){			//将各元素插入已经排好序的序列中
        if(A[i]<A[i-1]){		//若A[i]关键字小于前驱
            temp=A[i];			//用temp暂存A[i]
            //检查所有前面已排好序的元素
            for(j=i-1;j>=0&&A[j]>temp;--j)
                A[j+1] = A[j];	//所有大于temp的元素都向后挪位
            A[j+1] = temp;		//复制到插入的位置
        }
    }
}

带哨兵

//直接插入排序（带哨兵）
void InsertSort(int A[],int n){
    int i,j;
    for(i=2;i<=n;i++)	//一次将A[2]~A[n]插入到前面已排序序列
        //若A[i]关键码小于其前驱，将A[i]插入有序表
        if(A[i]<A[i-1]){
            A[0] = A[i];//复制为哨兵，A[0]不存放元素
            for(j=i-1;A[0]<A[j];--j)//从后往前查找待插入位置
                A[j+1]=A[j];//向后挪位
            A[j+1]=A[0];//复制到插入位置
        }
}

算法效率分析

空间复杂度：O(1)

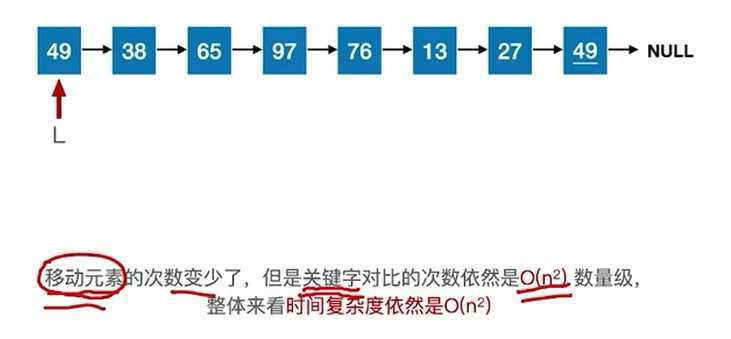
时间复杂度：主要来自对比关键字、移动元素，若有n个元素，则需要n-1趟处理。

最好情况

原本就有序的，共n-1趟处理，每一趟只需要对比关键字1次，不用移动元素

最好时间复杂度——O(n)

最坏情况

原本就逆序的，

第一趟：对比关键字2次，移动元素3次

第二趟：对比关键字3次，移动元素4次

。。，

第i趟：对比关键字i+1次，移动元素i+3次

最坏时间复杂度——O(n^2)

平均：

平均时间复杂度：O(n^2)

算法稳定性：稳定

优化——折半插入排序

先用折半查找找到应该插入的位置，在移动元素

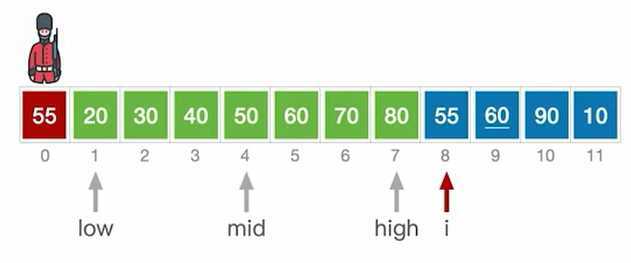
拿A[0]和mid比较，如果小了,low=mid+1,如果大了,high=mid-1

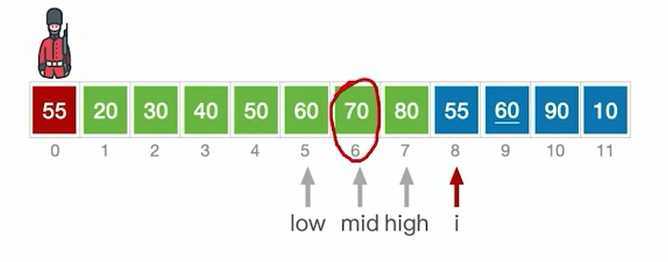
mid=low+high/2,大了,high=mid-1

大了，high=mid-1

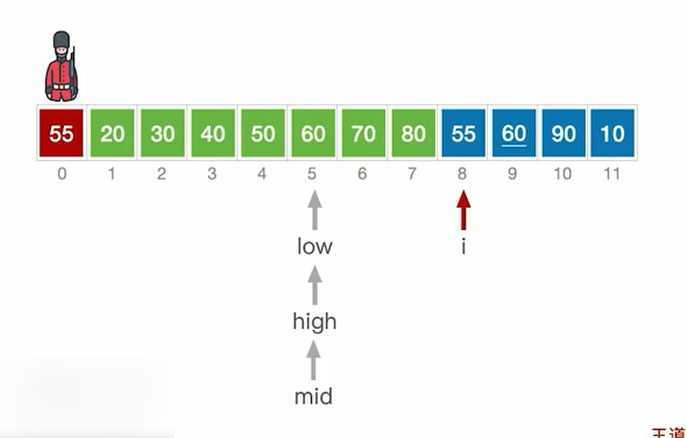
当low>high时折半查找停止，应将[low,i-1]内的元素全部右移，并将A[0]复制到low所指位置

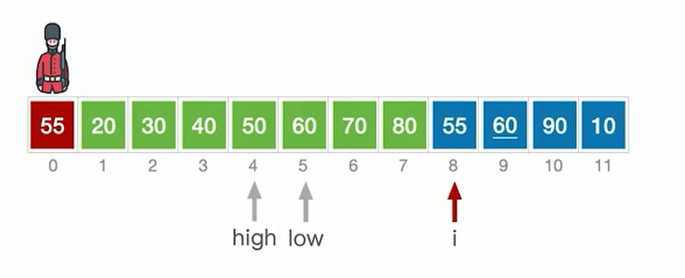
当A[mid] == A[0] 时，为了保证算法的“稳定性”，应继续在mid所指位置右边寻找插入位置

low>i-1时，不用移动元素

代码

//折半插入排序
void InsertSort(int A[] , int n){
    int i,j,low,high,mid;
    //依次将A[2]~A[n]插入到前面的已排序序列
    for(i=2;i<=n;i++){
        A[0]=A[i];				//将A[i]暂存到A[0]
        low=1;high=i-1;			//设置折半查找的范围
        while(low<=high){		//折半查找（默认递增有序）
            mid=(low+high)/2;	//取中间点
            if(A[mid]>A[0])		//查找左半子表
                high=mid-1;		//查找右半子表
            else
                low=mid+1;
        }
        for(j=i-1;j>=high+1;--j)
            A[j+1]=A[j];		//统一后移元素，留出插入位置
        A[high+1] = A[0];		//插入操作
    }
}

时间复杂度还是O(n^2)

对链表进行插入排序（自己实现）

知识回顾

插入排序

原文：https://www.cnblogs.com/jev-0987/p/13322138.html