知识点

BST的整个左子树中所有元素的值都是要小于根的值

BST的整个右子树中所有元素的值都是要大于根的值

递归解法

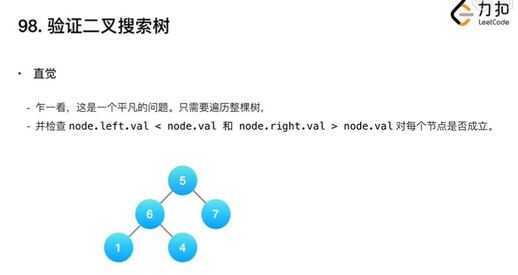
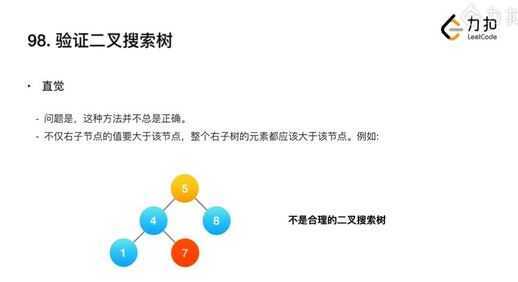
根据知识点，不能简单的判断是否左子小于根，右子大于根。

所以在遍历树的同时保留结点的上界和下界，在比较时不仅要比较结点的值，也要与上下界比较。

    public boolean helper(TreeNode node, Integer lowwer, Integer upper){
        if (node == null){
            return true;
        }
        int value = node.val;
        if (lowwer != null && lowwer >= value){
            return false;
        }
        if (upper != null && upper <= value){
            return false;
        }
        if (!helper(node.left, lowwer, value)){
            return false;
        }
        if (!helper(node.right, value, upper)){
            return false;
        }
        return true;
    }

    public boolean isValidBST1(TreeNode root) {
        return helper(root, null, null);
    }

时空间复杂度都是O(n)

中序遍历解法

二叉搜索树「中序遍历」得到的值构成的序列一定是升序的，这启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的，整棵树是二叉搜索树，否则不是

    public boolean isValidBST(TreeNode root) {
        double pre = - Double.MAX_VALUE;
        Deque<TreeNode> stack = new ArrayDeque<TreeNode> ();
        TreeNode temp = root;
        while (!stack.isEmpty() || temp != null){
            if (temp != null){
                stack.push(temp);
                temp = temp.left;
            }else {
                temp = stack.pop();
                if (temp.val <= pre){
                    return false;
                }
                pre = temp.val;
                temp = temp.right;
            }
        }
        return true;
    }

时空间复杂度都是O(n)

二叉树--验证BST（leetcode 98）

原文：https://www.cnblogs.com/swifthao/p/13321993.html