机器学习算法——SVM
1. 背景
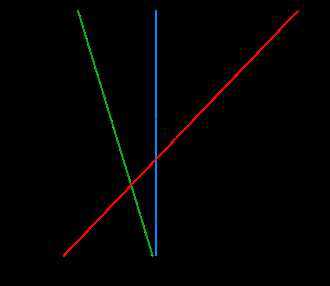
? 在线性分类任务中,对于同一个数据集,可能有多个分离超平面。例如在下图中,H2和H3都能够将白色点和黑色点分离开来,那么在这些分界面中,是否存在一个最优的分界面?一个直观的想法是,离所有点都比较远的分割面会是一个好的分割面。可以证明,这样的最优分割面是唯一的。因此SVM的目标就变成了寻找最大间隔分离超平面。
2. SVM推导
2.1 几何间隔和函数间隔
? 对于数据集\(\{x_i, y_i\}_{i=1}^N, y_i \in\{-1, +1\}\),分类器\(f(x)=w^Tx + b\),任意点\(x_i\)到分割面的几何间隔为:
\[d_i = \frac{y_i (w^T x_i + b)}{||w||}=y_i \left(\frac{w^T}{||w||}x + \frac{b}{||w||}\right), d=\min_{i\in\{1, 2, ..., N\}} d_i \label{geo_dist}\tag{1}
\]
从公式可知,如果成比例地改变\(w\)和\(b\),并不会影响\(d_i\)的值。定义函数间隔:
\[\hat{d}_i = ||w||d_i = y_i \left(w^T x_i+b\right), \hat{d}=\min_{i\in\{1, 2, ..., N\}} \hat{d}_i \label{func_dist}\tag{2}
\]
2.2 SVM原问题
? 最大间隔分离超平面问题可以表述为:
\[\max_{w,b} d \label{p1}\tag{3}\\
s.t \quad d_i = y_i \left(\frac{w^T}{||w||}x + \frac{b}{||w||}\right)\geq d, \forall i \in\{1, 2, ...,N\}
\]
将几何间隔替换为函数间隔,公式\(\ref{p1}\)可以写作:
\[\max_{w,b} \frac{\hat{d}}{||w||}\label{p2}\tag{4}\s.t \quad y_i \left(w^T x_i+b\right)\geq ||w||d = \hat{d} , \forall i \in\{1, 2, ...,N\}
\]
事实上函数间隔的取值并不会影响问题\(\ref{p2}\)的最优解(等比例放缩\(w\)和\(b\)不会影响不等式约束),取函数间隔\(\hat{d} = 1\),公式\(\ref{p2}\)变为:
\[\min_{w,b} \frac{1}{2}w^Tw \label{p3}\tag{5}\s.t \quad y_i (w^Tx_i+b)\geq 1, \forall i \in\{1, 2, ...,N\}
\]
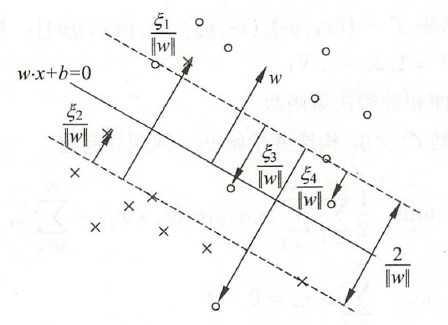
? 然而在某些情况下,最小函数间隔是1并不能成立(非线性可分情况),为了处理这种情形,引入松弛变量\(\xi_i\geq 0\),约束条件变为了函数间隔加上松弛变量要大于1,此时问题\(\ref{p3}\)变为:
\[\min_{w,b} \frac{1}{2}w^Tw+C\sum_{i=1}^N\xi_i \label{p4}\tag{6}\s.t \quad y_i (w^Tx_i+b)\geq 1 - \xi_i\\ \xi_i \geq 0, \quad \forall i \in\{1, 2, ...,N\}
\]
2.3 SVM对偶问题
? 写出问题\(\ref{p4}\)的拉格朗日函数:
\[\mathcal{L}(w, b, \xi, \alpha, \mu) = \frac{1}{2}w^Tw + C\sum_{i=1}^N\xi_i + \sum_{i=1}^N \alpha_i(1-\xi_i - y_i(w^T x_i + b)) - \sum_{i=1}^N \mu_i \xi_i, \alpha \geq 0 \label{Lagrangrian}\tag{7}
\]
原始问题为:\(\theta_p = \min_{w,b,\xi} \max_{\alpha} \mathcal{L}(w, b,\xi, \alpha)\),对偶问题为:\(\theta_d = \max_{\alpha} \min_{w,b,\xi}\mathcal{L}(w,b,\xi,\alpha)\)。求解对偶问题:
\[\nabla_w \mathcal{L}(w, b,\xi, \alpha) = w - \sum_{i=1}^N \alpha_i y_i x_i \label{grad}\tag{8}\\nabla_b \mathcal{L}(w, b,\xi, \alpha) = -\sum_{i=1}^N \alpha_i y_i \\nabla_{\xi_i} \mathcal{L}(w, b,\xi, \alpha) = C-\alpha_i-\mu_i , \forall i\in \{1, 2, .., N\}
\]
根据KKT条件得到:
\[w = \sum_{i=1}^N \alpha_i y_i x_i \label{kkt}\tag{9}\\sum_{i=1}^N \alpha_i y_i = 0 \C-\alpha_i - \mu_i = 0 \\alpha_i \geq 0 \\mu_i \geq 0\\alpha_i (1-\xi_i - y_i (w^Tx_i+b)) = 0 \\mu_i \xi_i = 0 \\xi_i \geq 0 \y_i (w^Tx_i +b)\geq 1 - \xi_i
\]
将KKT条件代入到对偶问题可得:
\[\max_\alpha \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^N \alpha_i \alpha_j y_i y_j x_i^Tx_j - \sum_{i=1}^N \alpha_i \label{p5}\tag{10}\s.t \quad \sum_{i=1}^N \alpha_i y_i = 0\0\leq \alpha_i \leq C , \quad \forall i \in \{1, 2, ..., N\}
\]
同时观察KKT条件可以得到:
- 如果\(\alpha_i < C\),一定有\(\xi_i = 0\)(\(\mu_i = C -\alpha_i \neq 0 \Longrightarrow \xi_i = 0\)),支持向量\(x_i\)恰好落在边界
- 如果\(\alpha_i = C, 0<\xi_i < 1\),则\(x_i\)分类正确,在间隔边界与超平面之间
- 如果\(\alpha_i = C, \xi_i = 1\),则\(x_i\)落在超平面上
- 如果\(\alpha_i = C, \xi_i > 1\),则\(x_i\)分类错误
2.4 SMO算法
2.4.1 更新公式
? 问题\(\ref{p5}\)仍然是一个二次规划问题,可以用一般的QP算法解决。但是对于SVM模型,有一种更加快速的优化算法。类似于坐标下降,SMO每次固定其他变量,只优化两个变量。
? 假设在问题\(\ref{p5}\)中,选择优化变量\(\alpha_1, \alpha_2\)。等式约束可以改写为:
\[\alpha_1 y_1 + \alpha_2 y_2 = -\sum_{i=3}^N \alpha_i y_i \triangleq \zeta \label{alpha1_alpha2}\tag{11}\\alpha_2 = \zeta y_2 -\alpha_1 y_1 y_2
\]
将待优化的变量分离出来,并将\(\alpha_2\)替换掉:
\[\begin{equation}\label{alpha1}\tag{12}
g(\alpha_1, \alpha_2) =& \frac{1}{2}\alpha_1^2 K_{11} + \frac{1}{2} \alpha_2^2 K_{22} + \alpha_1 \alpha_2 y_1 y_2 K_{12} + \alpha_1 y_1\sum_{i=3}^N \alpha_i y_i K_{1i} + \alpha_2 y_2\sum_{i=3}^N \alpha_i y_i K_{2i} \&+ \frac{1}{2}\sum_{i=3}^{N}\sum_{j=3}^N \alpha_i \alpha_j y_i y_j K_{ij} -(\alpha_1 + \alpha_2) - \sum_{i=3}^N \alpha_i \\
=& \frac{1}{2}\alpha_1^2 K_{11} + \frac{1}{2}\left( \zeta y_2 - \alpha_1 y_1 y_2\right)^2 K_{22} + \alpha_1 \left( \zeta y_2 - \alpha_1 y_1 y_2\right) y_1 y_2 K_{12}\&+ \alpha_1 y_1 v_1 + \left( \zeta y_2 - \alpha_1 y_1 y_2\right)y_2 v_2 -\alpha_1 - \zeta y_2 + \alpha_1 y_1 y_2 + \mathrm{const} \=& \frac{1}{2} \left( K_{11} - 2K_{12} + K_{22}\right)\alpha_1^2 + \left[\zeta y_1(K_{12} - K_{22}) + y_1(v_1 -v_2)+(y_1 y_2 - 1) \right]\alpha_1 + \mathrm{const}
\end{equation}
\]
因此有:
\[\frac{\partial g}{\partial \alpha_1} = (K_{11} - 2K_{12}+K_{22})\alpha_1 + \zeta y_1(K_{12} - K_{22}) + y_1(v_1 -v_2)+(y_1 y_2 - 1) \label{grad_alpha1}\tag{13}
\]
其中:
\[v_1 = \sum_{i=3}^N \alpha_i y_i K_{1i} = \sum_{i=1}^N \alpha_i^{old} y_i K_{1i} - \alpha_1^{old}y_1 K_{11} - \alpha_2^{old}y_2 K_{12} = f(x_1) - \alpha_1^{old}y_1 K_{11} - \alpha_2^{old}y_2 K_{12} - b \label{v}\tag{14}\v_2 = \sum_{i=3}^N \alpha_2 y_i K_{2i} = \sum_{i=1}^N \alpha_i^{old} y_i K_{2i} - \alpha_1^{old}y_1 K_{21} - \alpha_2^{old}y_2 K_{22} = f(x_2) - \alpha_1^{old}y_1 K_{21} - \alpha_2^{old}y_2 K_{22} - b
\]
所以:
\[\begin{aligned}
v_1 - v_2 &= f(x_1) - f(x_2) - \alpha_1^{old}y_1(K_{11}-K_{21}) - (\zeta y_1 - \alpha_1 y_1 y_2)y_2(K_{12}-K_{22}) \\
&= f(x_1) - f(x_2) - \alpha_1^{old}y_1(K_{11} - 2K_{12} + K_{22}) - \zeta y_1 y_2 (K_{12} - K_{22}) \label{diff_v}\tag{15}
\end{aligned}
\]
带入到公式\(\ref{grad_alpha1}\)得到:
\[\begin{aligned}
\frac{\partial g}{\partial \alpha_1} &= (K_{11} - 2K_{12}+K_{22})\alpha_1^{new} + \zeta y_1(K_{12} - K_{22}) \&+ y_1( f(x_1) - f(x_2) - \alpha_1^{old}y_1(K_{11} - 2K_{12} + K_{22}) - \zeta y_1 y_2 (K_{12} - K_{22}))+(y_1 y_2 - 1)\&= (K_{11} - 2K_{12}+K_{22})(\alpha_1^{new}-\alpha_1^{old}) + y_1 ((f(x_1) - y_1)-(f(x_2) -y_2)) \&= (K_{11} - 2K_{12}+K_{22})(\alpha_1^{new}-\alpha_1^{old}) - y_1 (E_1-E_2) \label{grad_alpha1_2}\tag{16}
\end{aligned}
\]
令该导数为0,得到:
\[\alpha_1^{new} = \alpha_1^{old} + \frac{y_1(E_1-E_2)}{K_{11} - 2K_{12}+K_{22}}\label{alpha1_new}\tag{17}
\]
2.4.2 裁剪
? 现在考虑对偶问题中的框约束。\(\alpha_1, \alpha_2\)的等式约束\(\ref{alpha1_alpha2}\)可以写作:
\[\alpha_1^{new} y_1 + \alpha_2^{new} y_2 = \zeta = \alpha_1^{old} y_1 + \alpha_2^{old} y_2 \label{old_new}\tag{18}
\]
对\(y_1, y_2\)分类讨论:
-
当\(y_1 \neq y_2\)时,\(\alpha_{1}^{new}-\alpha_2^{new} = k = \alpha_1^{old}-\alpha_2^{old}\)
- \(k>0\Longrightarrow \alpha_1 \in \left[k, C\right]\)
- \(k < 0\Longrightarrow \alpha_1 \in \left[0, C+k\right]\)
因此有\(L = \max\{0, \alpha_1^{old}-\alpha_2^{old}\}, H = \min\{C, C + \alpha_1^{old}-\alpha_2^{old}\}\)
-
当\(y_1 = y_2\)时,\(\alpha_{1}^{new}+\alpha_2^{new} = k = \alpha_1^{old}+\alpha_2^{old}\),同上一种情况可得\(L = \max\{0, \alpha_1^{old}+\alpha_2^{old}-C\}, H = \min\{C, \alpha_1^{old}+\alpha_2^{old}\}\)
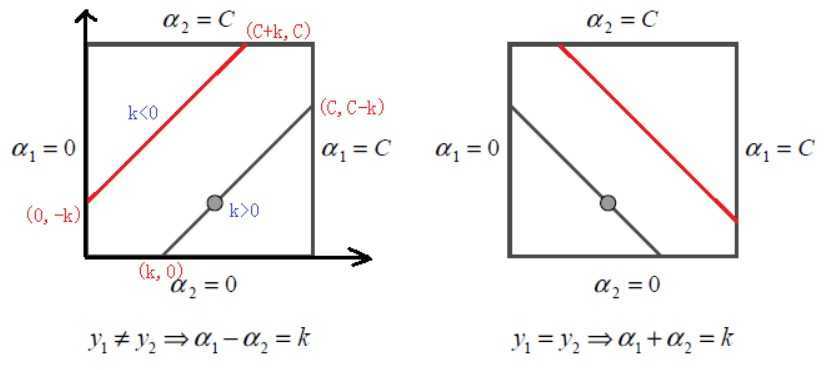
对\(\alpha_1^{new}\)的裁剪过程如下:
\[\begin{equation}\label{clip}\tag{19}
\alpha_1^{new,cliped}=
\begin{cases}
H&,\alpha_1^{new}\geq H \\alpha_1^{new}&, L<\alpha_1^{new}< H\L&, \alpha_1^{new}\leq L
\end{cases}
\end{equation}
\]
在计算出\(\alpha_1^{new}\)之后,代入\(\ref{old_new}\)可以得到:
\[\alpha_2^{new} = \alpha_2^{old}+y_1 y_2 (\alpha_1^{old}-\alpha_2^{old}) \label{alpha2_new}\tag{20}
\]
2.4.3 优化变量的选择
? \(\alpha_i, \alpha_j\)的选择。在选择第一个变量\(\alpha_i\)时,找出违反KKT条件最严重的,这样能加快优化过程。KKT条件具体是:
\[\begin{aligned}
\alpha_{i} &=0 \Leftrightarrow y_{i} f\left(x_{i}\right) \geqslant 1 \0<\alpha_{i} &<C \Leftrightarrow y_{i} f\left(x_{i}\right)=1 \\alpha_{i} &=C \Leftrightarrow y_{i} f\left(x_{i}\right) \leqslant 1
\end{aligned}
\]
其中\(f\left(x_{i}\right)=\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)+b\)。在检验时,首先在支持向量中寻找,即\(0<\alpha_{i} <C\),如果支持向量都满足KKT条件,则在全部数据集中寻找。在给定了第一个变量时,第二个变量\(\alpha_j\)的选择要使\(\alpha_j\)有足够大的变化,即使\(|E_i -E_j|\)最大。
2.4.4 偏移\(b\)和误差\(E_i\)的更新
? 根据KKT条件可知,当向量\(x_i\)是支持向量时有\(y_{i} f\left(x_{i}\right)=1\)。在计算完\(\alpha_1^{new}\)之后,如果\(0<\alpha_1^{new}<C\):
\[\sum_{i=1}^N y_i \alpha_i K_{1i} + b= y_1
\]
于是有:
\[b = y_1 - \sum_{i=1}^N y_i \alpha_i^{old} K_{1i} + y_1K_{11}(\alpha_1^{old}-\alpha_1^{new})+y_2 K_{12}(\alpha_2^{old} - \alpha_2^{new})
\]
代入\(E_1 = y_1 - f(x_1) = y_1 - \sum_{i=1}^N \alpha_i^{old}y_i K_{1i}-b^{old}\)得到:
\[b^{new} = E_1 + y_1K_{11}(\alpha_1^{old}-\alpha_1^{new})+y_2 K_{12}(\alpha_2^{old} - \alpha_2^{new}) + b^{old}
\]
同样地当\(0<\alpha_2^{new}<C\),有:
\[b_{2}^{\text {new }}=E_{2}+y_{1} K_{12}\left(\alpha_{1}^{\text {old }}-\alpha_{1}^{\text {new }}\right)-y_{2} K_{22}\left(\alpha_{2}^{\text {old }}-\alpha_{2}^{\text {new }}\right)+b^{\text {old }}
\]
当\(\alpha_1^{new}, \alpha_2^{new}\)是0或者C时,选择\(\frac{b_1^{new} + b_2^{new}}{2}\)作为更新值(因为在\([b_1^{new}, b_2^{new}]\)中的数都能满足KKT条件,选中点作为近似)
? 当更新完\(\alpha_1, \alpha_2, b\)之后,误差\(E_i\)更新为:
\[E_{i}^{\text {new }}=y_i - \sum_{S} y_{j} \alpha_{j} K\left(x_{i}, x_{j}\right)+b^{\text {new }}
\]
其中\(S\)是支持向量的集合。
3. SVM的python实现
【机器学习】svm
原文:https://www.cnblogs.com/vinnson/p/13328143.html


