Trie——解决字符串搜索、异或最值问题

Trie——解决字符串搜索、异或最值问题

• 在说到Trie之前，我们设想如下问题：

给我们1e5个由小写字母构成的不重复的字符串，每个字符串长度不超过6，之后是1e5次查询操作，每次给我们一个字符串，要求我们判断这个字符串是否出现过，如果是则求出它是多少个其他的字符串的前缀，并在之后的操作中无视这个字符串（删除）。

• 查询是否出现这个可以用set或者hash，但是前缀，，其实也有办法，但是这里要介绍的方法是使用一种易于理解的数据结构——Trie

建立Trie

• 字典树Trie的结构比较自然，如对于字符串集合{"abca", "ab", "bcd", "abcde", "bcde", "bcdf"}，可以建立一棵这样的Trie：

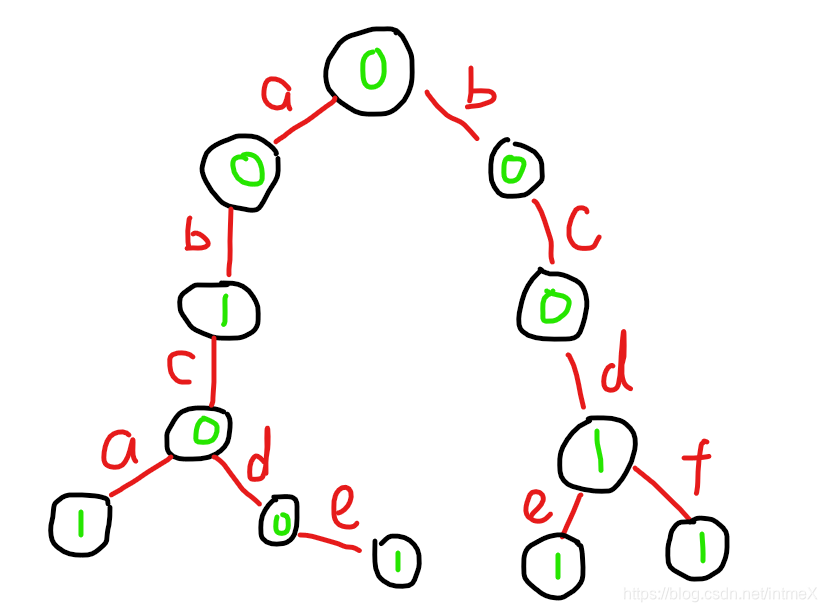
可知：

- 每一条边代表一个字符
- 节点不为0代表从根节点到此为一个完整的字符串

实现的方法也比较简单，建立一棵单向树，每个节点都有

• 26个子节点（所有小写字母）；

• 一个isstr，bool值，代表这里是否为一个字符串的结束

• 一个vis，int值，代表到这里已经有多少个字符串遍历过（是多少字符串的前缀）

一开始树为空，我们每得到一个字符串，就从它的第一个字符开始，从根节点遍历，没有对应的节点就创建，同时把所经过的节点的vis值加一，到最后字符串终止时，在终止的节点处置isstr为true。

更多操作

1.查询

从树的形状就可以看出，这是一棵专门查询字符串存在与否的数据结构（同时也付出了巨大的空间代价）。查询操作很简单，从根节点开始，按照要查询的字符串的每一位来遍历，如果遇到空节点或者终止时的节点的isstr为false，则字符串不存在，否则存在。

2.查询某个串是多少个字符串的前缀

这个就是读取要查询的字符串的终止节点的vis值即可

3.删除某个字符串

首先查询成功之后，我们从底部开始回溯删除这个串的信息，将终止节点的isstr置为false，同时将路过的vis值减一，如果vis值减为0则将将此节点在其父节点中删除即可。

01Trie解决xor最值问题

原题链接

题意

给我们一个序列A和序列B，要求我们找到B序列的一种排列，使得

中的序列C字典序最小，并输出序列C，长度<=3e5，每个数小于2^30

思路

• 首先按照运算规则C xor B == A意味着A xor B == C 也就是说 寻找一种B的排列，使得A逐个与B异或的结果的字典序最小

• 3e5基本不可能在其他操作中间搞什么排序了，应该从异或运算的结果出发，我们追求结果的字典序最小，也就是说，对于每个Ai，我们都要找到一个Bj，使得其异或结果最小。这个如果直接找的话，是比较难的。但是如果使用Trie的话，可以直接求得每一个Ai的最小结果，方法如下：

  • 对B序列建立一棵只包含01字符的Trie（也就是二叉树），我们规定A与B的每一个数都是30位二进制数，左边补零，从左边的第一位开始建树。

  • B序列的01Trie建好之后，对A序列从1到n每个数都按位在Trie中遍历，一开始先设ans为0，之后优先走与当前自己的二进制位相同的边，如果没有则让ans或上这一位的1。（确保ans尽可能地小）

  • 之后输出这个ans，并将走过的路线所代表的Bi删除掉就可以

• 可以看出时间复杂度为

  \[O(30*n) \]

• 对空间复杂度来说，不要使用满二叉树的存储方式，使用动态开点的方式，空间复杂度不超过

  \[O(30*n) \]

01Trie代码如下：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

int n;
int aa[10000005][2] = {{0}}, vv[10000005][2] = {{0}}, co = 1;
int A[300005] = {0};

void add(int x)
{
	int o = 1;
	for (int i = 29; i >= 0; --i)
	{
		int bitt = (x >> i) & 1;
		if (!aa[o][bitt])
		{
			aa[o][bitt] = ++co;
		}
		++vv[o][bitt];
		o = aa[o][bitt];
	}
}

int trie(int x)
{
	int o = 1, ans = 0;
	for (int i = 29; i >= 0; --i)
	{
		int bitt = (x >> i) & 1;
		if (vv[o][bitt])
		{
			--vv[o][bitt];
			o = aa[o][bitt];
			
		}
		else
		{
			--vv[o][bitt ^ 1];
			o = aa[o][bitt ^ 1];
			ans |= (1 << i);
		}
	}
	return ans;
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d", &A[i]);
	}
	for (int i = 1; i <= n; ++i)
	{
		int xx;
		scanf("%d", &xx);
		add(xx);
	}
	for (int i = 1; i < n; ++i)
	{
		printf("%d ", trie(A[i]));
	}
	printf("%d", trie(A[n]));
	return 0;
}

Trie——解决字符串搜索、异或最值问题

原文：https://www.cnblogs.com/int-me-X/p/13332288.html