题目来源于 LeetCode 204.计数质数,简单来讲就是求“不超过整数 n 的所有素数个数”。
一般来讲,我们会先写一个判断 a 是否为素数的 isPrim(int a) 函数:
bool isPrim(int a){
for (int i = 2; i < a; i++)
if (a % i == 0)//存在其它整数因子
return false;
return true;
}
然后我们会写一个 countIsPrim(int n) 来计算不超过 n 的所有素数个数:
int countPrimes(int n) {
int ans = 0;
for (int i = 2; i < n; i++)
if (isPrim(i)) ans++;
return ans;
}
显然这两个嵌套的 for 循环时间复杂度是 \(O(n^2)\) ,但是这样写有两个主要的问题:
isPrim() 函数的计算冗余。首先,举个例子引入一下因子的对称性:
12 = 2 × 6
12 = 3 × 4
12 = sqrt(12) × sqrt(12)
12 = 4 × 3
12 = 6 × 2
所以当循环判断一个数 \(a\) 是否有除了 1 和它本身之外其余的因子时,我们只需要将循环变量终止在 \(\sqrt a\) 的位置,而非 [2, a) 的所有数。
countPrimes(int n)函数的计算冗余。例如,一旦我们判断2为质数那么所有2的倍数一定都是质数,如果我们知道3是质数,那么所有3的倍数也一定都是质数。所以如果我们将 [2, n) 的数都进行一次 isPrim() ,那么将带来巨大的时间浪费。
我们在这里,先将第一个问题解决,即优化 isPrim() 函数:
bool isPrim(int n){
//根据因子对称性
for (int i = 2; i * i <= n; i++){
if (n % i == 0)//存在其它整数因子
return false;
}
return true;
}
这个算法的中文叫作“埃拉托斯特尼筛法”,听起来很复杂,但是并不难理解,本质上就是把常规思路反过来,如下面动图所示:
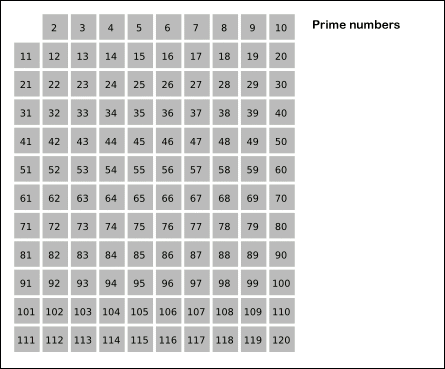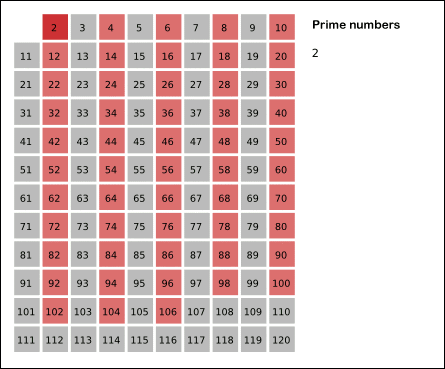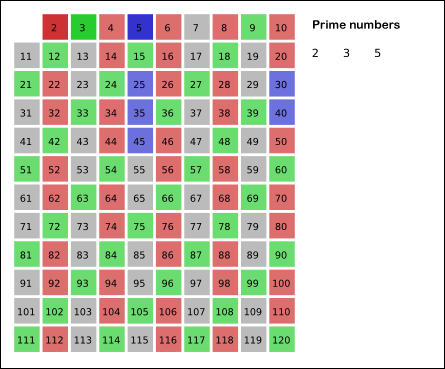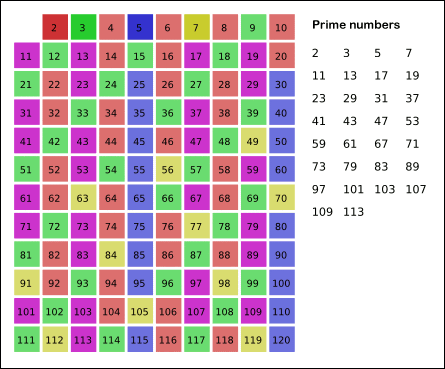
下面我们逐渐引出该算法的全貌:
常规思路就是将区间为 [2, n) 的数都遍历一遍,在过程中累加素数的个数。上述问题二已经说明了其低效性,根据“如果 i 是质数,那么所有 i 的倍数都不是质数”,我们做出优化:
int countPrimes(int n) {
vector<int> IsPrim(n + 1, true);
for (int i = 2; i < n; i++){
if (isPrim[i]){
//如果i是质数,那么所有i的倍数都不是质数
for (int j = 2 * i; j < n; j += i){
IsPrim[j] = false;
}
}
}
//遍历一遍计算结果
int ans = 0;
for (int i = 2; i < n; i++){
if (IsPrim[i]) ans++;
}
return ans;
}
这段代码展现了该算法的整体思路,但是还有两个细节可以优化:
for (int i = 2; i * i < n; i++) 。for (int j = i * i; j < n; j += i) 。举个例子, n = 25 ,当 i = 4 时算法会标记 4 × 2 = 8,4 × 3 = 12 等等数字,但是这两个数字已经被 i = 2 和 i = 3 的 2 × 4 和 3 × 4 标记了。所以我们可以从平方项开始遍历。到这里,Sieve of Eratosthenes 算法就已经实现了,下面给出完整的代码:
int countPrimes(int n) {
vector<int> prims(n + 1, 1);
for (int i = 2; i * i < n; i++){
if (isPrim[i]){
//如果i是质数,那么所有i的倍数都不是质数
for (int j = i * i; j < n; j += i){
prims[j] = 0;
}
}
}
//遍历一遍计算结果
int ans = 0;
for (int i = 2; i < n; i++){
if(prims[i]) ans++;
}
return ans;
}
该算法的时间复杂度为 \(O(nloglogn)\) ,下面给出三个公式和证明:
\(Prerequisite\).
调和级数(Harmonic series)是一个发散的无穷级数,当 \(n\) 趋近于无穷大时,有一个近似公式:
其中 \(\gamma\) 为欧拉常数,\(\gamma \approx 0.57721\)
泰勒级数(Taylor series)是1715年英国数学家布鲁克·泰勒提出的,在零点的导数求得的泰勒级数又叫麦克劳林级数,一个常用的泰勒级数如下:
对任意 \(x \in [-1,1)\) 都成立。
欧拉乘积公式(Euler product)是著名的瑞士数学家欧拉于1737年在俄罗斯的圣彼得堡科学院发表的重要公式,为数学家研究素数的分布奠定了基础,即:
其中 \(n\) 是自然数,\(p\) 为素数。
\(Prove.\)
该算法的运行时间可以看作筛除的次数之和:
显然我们需要想办法处理后面的质数倒数和。我们拿出欧拉乘机公式,将所有的 \(s\) 用1来代替:
两侧同时取对数:
由于 \(-1< p^{-1} < 1\) ,所以对上面右侧求和的每一项进行泰勒展开得到:
当 \(p\) 趋向于无穷时,该级数收敛于 \(\frac{1}{p}\) ,得到:
故得到:
上式左侧带入调和级数得到:
到这里就成功处理掉了质数倒数和,所以时间复杂度为 \(O(nloglogn)\) 。
未改进版 \(isPrim()\) 、改进版 \(isPrim()\) 、高效算法三者耗时对比如下,可以看出来差距还是很大的:
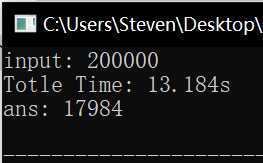
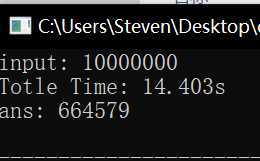
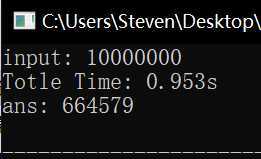
“计数质数”问题的常规思路和Sieve of Eratosthenes算法分析
原文:https://www.cnblogs.com/pxsong/p/SieveofEratosthenes.html