有一个A数组
a[1],a[2],a[3],a[4],…………
有一个C数组 是树状数组里存的东西,每个结点掌管[x-lowbit(x)+1,x]
c[1]=a[1]
c[2]=a[1]+a[2]
c[3]=a[3]
c[4]=a[1]+a[2]+a[3]+a[4]
c[5]=a[5]
c[6]=a[5]+a[6]
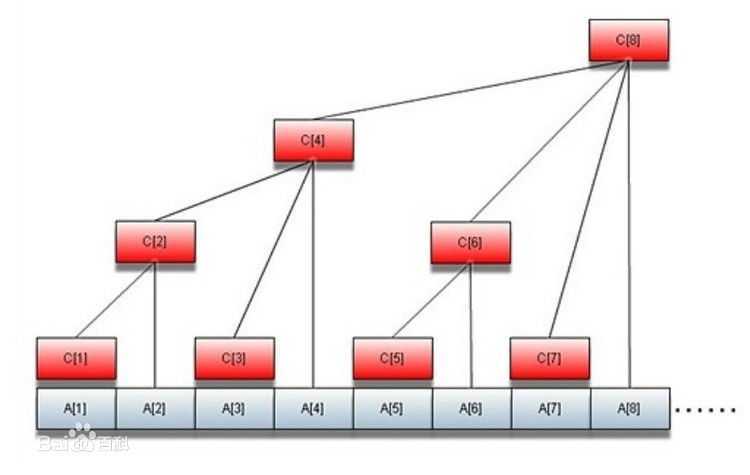
change: Ax增加val,Ax及其父节点都要增加val。
search: 询问[l,r]的权值和 可以用统计好的前缀和数组sum进行sum[r]-sum[l-1]
? 这里用到的sum,从x开始加,每次加完将x=x-lowbit(x),直到x为1
//lowbit(i)= ((i)&(-i))
void change(int x,int val)
{
for(int i=x;i<=n;i+=low(i))
c[i]+=val;
}
void search(int x)
{
int sum=0;
for(int i=x;i;i-=lowbit(i))
sum+=c[i];
return sum;
}
区间修改:差分思想,l处+val,r+1处-val
单点询问:
int main() {
n=read(),m=read();
for(int i=1;i<=n;i++)
a[i]=read(),sum[i]=sum[i-1]+a[i];
for(int i=1;i<=m;i++) {
int opt=read(),l=read(),r=read();
if(opt==1) {//区间加
ll k=read();
T1.add(l,k);T1.add(r+1,-k);
T2.add(l,l*k);T2.add(r+1,-(r+1)*k);
}
else {//区间查询
ll ans=sum[r]-sum[l-1];
ans+=(r+1)*T1.query(r)-T2.query(r);
ans-=l*T1.query(l-1)-T2.query(l-1);
printf("%lld\n",ans);
}
}
return 0;
}
https://www.cnblogs.com/jason2003/p/9676729.html
x&(~x+1
t[x]=lowbit(x)
差分数组d[i]=a[i]-a[i-1]; a[0]=0;__>a[i]=d[1]+……+d[i]
一个节点p掌管[l,r],mid=(l+r)/2,
左儿子掌管[l,mid] 右儿子掌管[mid+1,r]
每个点的信息可由子节点更新,且都为二叉树,所以我们用p*2来记录左儿子,P*2+1来记录右儿子
inline void build(int i,int l,int r){//递归建树
tree[i].l=l;tree[i].r=r;
if(l==r){//如果这个节点是叶子节点
tree[i].sum=input[l];
return ;
}
int mid=(l+r)>>1;
build(i*2,l,mid);//分别构造左子树和右子树
build(i*2+1,mid+1,r);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//刚才我们发现的性质
return ;
}
1、如果这个区间被完全包括在目标区间里面,直接返回这个区间的值
2、如果这个区间的左儿子和目标区间有交集,那么搜索左儿子
3、如果这个区间的右儿子和目标区间有交集,那么搜索右儿子
inline int search(int i,int l,int r){
if(tree[i].l>=l && tree[i].r<=r)//如果这个区间被完全包括在目标区间里面,直接返回这个区间的值
return tree[i].sum;
if(tree[i].r<l || tree[i].l>r) return 0;//如果这个区间和目标区间毫不相干,返回0
int s=0;
if(tree[i*2].r>=l) s+=search(i*2,l,r);//如果这个区间的左儿子和目标区间又交集,那么搜索左儿子
if(tree[i*2+1].l<=r) s+=search(i*2+1,l,r);//如果这个区间的右儿子和目标区间又交集,那么搜索右儿子
return s;
}
inline void add(int i,int dis,int k){
if(tree[i].l==tree[i].r){//如果是叶子节点,那么说明找到了
tree[i].sum+=k;
return ;
}
if(dis<=tree[i*2].r) add(i*2,dis,k);//在哪往哪跑
else add(i*2+1,dis,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;//返回更新
//一般如果需要求最大值或其他就改变这一句
return ;
}
区间修改和单点查询,我们的思路就变为:如果把这个区间加上k,相当于把这个区间涂上一个k的标记,然后单点查询的时候,就从上跑道下,把沿路的标记加起来就好。
这里面给区间贴标记的方式与上面的区间查找类似,原则还是那三条,只不过第一条:如果这个区间被完全包括在目标区间里面,直接返回这个区间的值变为了如果这个区间如果这个区间被完全包括在目标区间里面,讲这个区间标记k
inline void add(int i,int l,int r,int k){
if(tree[i].l>=l && tree[i].r<=r){//如果这个区间被完全包括在目标区间里面,讲这个区间标记k
tree[i].sum+=k;
return ;
}
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
}
void search(int i,int dis){
ans+=tree[i].num;//一路加起来
if(tree[i].l==tree[i].r)
return ;
if(dis<=tree[i*2].r)
search(i*2,dis);
if(dis>=tree[i*2+1].l)
search(i*2+1,dis);
}
的时候,我们按照如下原则:
1、如果当前区间被完全覆盖在目标区间里,讲这个区间的sum+k*(tree[i].r-tree[i].l+1)
2、如果没有完全覆盖,则先下传懒标记
3、如果这个区间的左儿子和目标区间有交集,那么搜索左儿子
4、如果这个区间的右儿子和目标区间有交集,那么搜索右儿子
void add(int i,int l,int r,int k)
{
if(tree[i].r<=r && tree[i].l>=l)//如果当前区间被完全覆盖在目标区间里,讲这个区间的sum+k*(tree[i].r-tree[i].l+1)
{
tree[i].sum+=k*(tree[i].r-tree[i].l+1);
tree[i].lz+=k;//记录lazytage
return ;
}
push_down(i);//向下传递
if(tree[i*2].r>=l)
add(i*2,l,r,k);
if(tree[i*2+1].l<=r)
add(i*2+1,l,r,k);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
return ;
}
void push_down(int i)
{
if(tree[i].lz!=0)
{
tree[i*2].lz+=tree[i].lz;//左右儿子分别加上父亲的lz
tree[i*2+1].lz+=tree[i].lz;
init mid=(tree[i].l+tree[i].r)/2;
tree[i*2].data+=tree[i].lz*(mid-tree[i*2].l+1);//左右分别求和加起来
tree[i*2+1].data+=tree[i].lz*(tree[i*2+1].r-mid);
tree[i].lz=0;//父亲lz归零
}
return ;
}
void push_down(int i)
{
if(tree[i].lz!=0)
{
tree[i*2].lz+=tree[i].lz;//左右儿子分别加上父亲的lz
tree[i*2+1].lz+=tree[i].lz;
init mid=(tree[i].l+tree[i].r)/2;
tree[i*2].data+=tree[i].lz*(mid-tree[i*2].l+1);//左右分别求和加起来
tree[i*2+1].data+=tree[i].lz*(tree[i*2+1].r-mid);
tree[i].lz=0;//父亲lz归零
}
return ;
}
原文:https://www.cnblogs.com/zjy0217/p/13353486.html