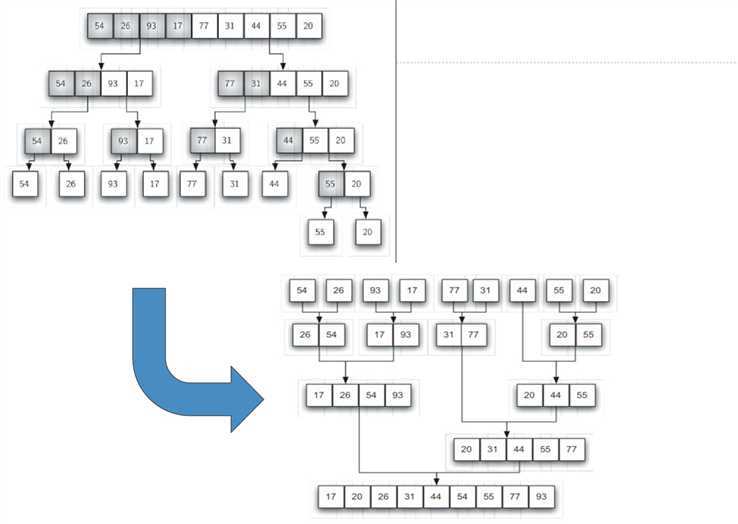
算法处理思路:将数据表持续分裂成两半,对两半分别进行归并排序。可以用递归的思想解决。
其中,递归结束的基本条件是数据表仅有1个数据项。
缩小规模:将数据表持续分裂为相等的两半,规模减小为原来的1/2.
调用自身:将两半分别调用自身排序,然后将分别排好序的两半进行归并,得到排好序的数据表。
def merge_sort(lst): if len(lst) <= 1: return lst middle = len(lst) // 2 left = merge_sort(lst[:middle]) right = merge_sort(lst[middle:]) merged = [] while left and right: if left[0] <= right[0]: merged.append(left.pop(0)) else: merged.append(right.pop(0)) merged.extend(right if right else left) return merged if __name__ == "__main__": alist = [54, 26, 93, 17, 77, 31, 44, 55, 20] print(merge_sort(alist))
分裂过程时间复杂度:O(log n)
归并归并过程时间复杂度O(n)
因此归并排序的时间复杂度O(n log n),并且十分稳定。
但是,归并排序增加了额外1倍的存储空间用于归并。因此对于大规模数据集,需要慎重考虑
原文:https://www.cnblogs.com/yeshengCqupt/p/13367151.html