从0开始的机器学习——线性回归篇（5）

实现多元线性回归

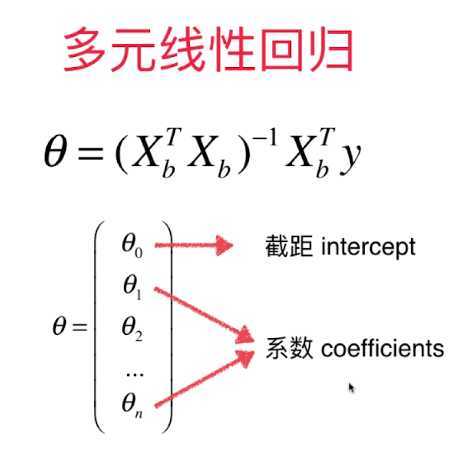
计算时需要把截距和系数分开计算。因为系数对于整个线性回归的影响是比较大的，而截距的影响比较小。需要在计算时加以区分。

代码实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()

X = boston.data
y = boston.target

X = X[y < 50.0]
y = y[y < 50.0]

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size = 0.2,random_state = 666)

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X_train,y_train)

然后可以查看对应的参数值和评价标准：

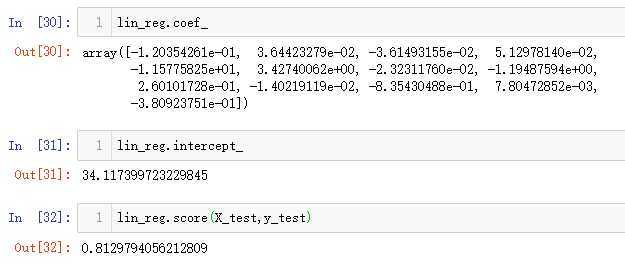
coef_是参数，intercept_是截距。后面带一个_小尾巴是表示不是用户直接输入的数据，但是由用户输入的数据计算得来，并且用户可能要查看的数据，就带一个小尾巴。

knn算法也可以解决回归问题，下面尝试一下knn算法解决回归问题。

from sklearn.neighbors import KNeighborsRegressor

knn_reg = KNeighborsRegressor()
knn_reg.fit(X_train,y_train)
knn_reg.score(X_test,y_test)

可以发现这个评价结果相比线性回归是差了很多的，这是因为knn算法中有很多超参数的值需要调整才能达到最好的拟合。

接下来使用网格搜索来寻找最合适的超参数值。

from sklearn.model_selection import GridSearchCV

param_grid = [
    {
        ‘weights‘:[‘uniform‘],
        ‘n_neighbors‘ : [i for i in range(1,11)]
    },
    {
        ‘weights‘:[‘distance‘],
        ‘n_neighbors‘:[i for i in range(1,11)],
        ‘p‘:[i for i in range(1,6)]
    }   
]

knn_reg = KNeighborsRegressor()
grid_search = GridSearchCV(knn_reg,param_grid,verbose=2)
grid_search.fit(X_train,y_train)

可以看出来最合适的p值是5，使用闵可夫斯基距离。调用best_score_查看此时的评价标准是0.63，但是此时的评价标准和线性回归的标准不是一个，这个评价都没有用到测试数据。

第二个是和线性回归法一致的评价标准，此时结果大约为0.7，相较于线性回归法还是要差了一些的。

可以发现，调用sklearn中封装好的机器学习方法的流程：引入→创建对应的对象→调用fit()方法传入train数据进行训练→查看评估标准score或者预测值predict

从0开始的机器学习——线性回归篇（5）

原文：https://www.cnblogs.com/xiyoushumu/p/13365520.html