最容易想到的一种做法,定义一个二维数组w来存;
如下图
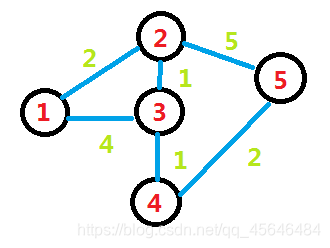
因为1和2之间有一条边权为2的边,那我们在(1,2),(2,1)填上2。
同理,因为2和3之间有一条边权为1的边,那我们在(2,3),(3,2)填上1。
以此类推,最后在没有边相连的两节点间填上-1;
写成代码就是
const int N=1000+5;
int w[N][N];
int x,y,z;
void Init()
{
scanf("%d%d",&n,&m);
int i,j;
for(i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
w[x][y]=w[y][x]=z;
}
return;
}
遍历方式
for(int i=1;i<=n;i++)
{
if(w[u][i]==-1) continue;
...;
}
邻接矩阵慢就慢在要遍历很多无用的点,那我们能不能把以一个点出发,所有有用的点都存在一个数组里呢?
显然可以:
//城市x与城市y有长度为z的路
int a[N][N],w[N][N];
int x,y,z;
void Init()
{
scanf("%d%d",&n,&m);
int i,j;
for(i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
a[x][++a[x][0]]=y;
a[y][++a[y][0]]=x;
w[x][y]=w[y][x]=z;
return;
}
}
遍历方式:
for(int i=1;i<=a[x][0];i++)
{
y=a[x][i]; z=w[x][y];
...;
}
优点:
缺点
适用算法
紧接上文邻接矩阵的优化,---->如果在存以一个点出发,所有有用的点的编号时同时存下边权,那不就可以省空间了吗。
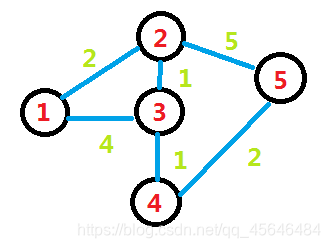
如上图,是这么存的
因为1和2之间有一条边权为2的边,那我们在1开头的那一行的末尾填上(2,2)
第一个表边号,第二个表边权。(反过来当然也可以,个人喜好);
由于不知道一个点有多少个与之相连的点,于是用stl的动态数组vector来存。
这样省了空间,只不过常数会大一点。
const int N=50000+5;
vector< pair<int,int> > a[N];
void Init()
{
int i,j;
int x,y,z;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
a[x].push_back(make_pair(y,z));
a[y].push_back(make_pair(x,z));
}
return;
}
遍历方式
for(int i=0;i<a[x].size();i++)
{
y=a[x][i].first; z=a[x][i].second;
...;
}
为了解决vector常数较大的弊端,大佬们发明了链式前向星。
链式前向星用于存储有向边,一条无向边分为两条有向边来存。

开一个统一的数组来存储边的信息。
那么一条边要存几个信息呢?
一是通向的节点ver,二是边权edge,三是以该点为起点的下一条边的编号Next。
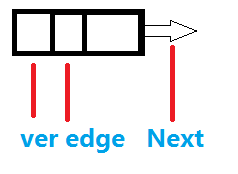
还要另外开一个数组one,存储以该点为出发点的第一条边的编号(实际上是最后一条边),这样就可以从该边开始,不断调用其Next,把以该点为出发点所有边遍历了;
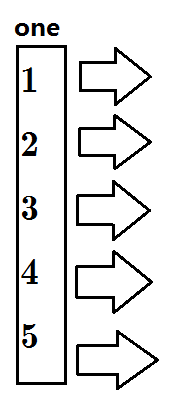
没有加入一条边,所有one指向0;

tot++;//tot是内存池
one[1]=tot; //接入
ver[tot]=2;
edge[tot]=0;
以1开头已经有一条边了,那么如何接入该边呢?
先遍历1开头的边,找到最后一边,将其Next指向tot。
时间复杂度是和边的数量正相关的,显然当以1为起点的边非常多时,程序会特别慢,所以我们考虑思路2.
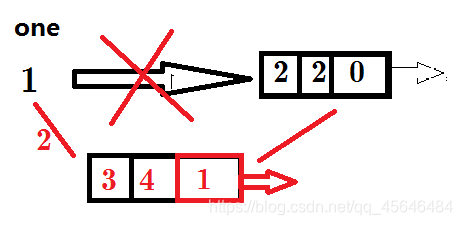
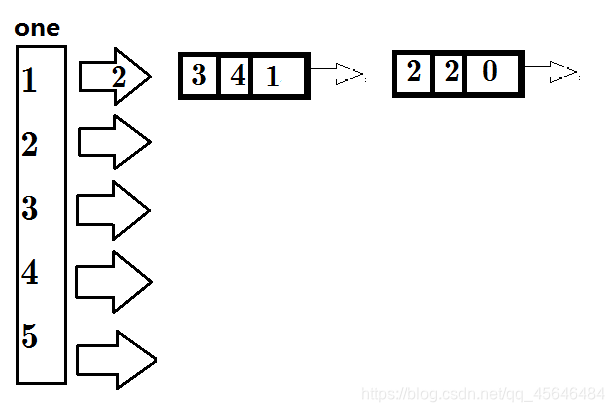 如何操作?
如何操作?
先将新边的Next指向one指向的边(防止其丢失),
再将one指向新边的编号。
于是我们得到了通用的添边函数
const int N=10000+5;
int one[N];
int ver[2*N],edge[2*N],Next[2*N];
int tot=0;
void AddEdge(int a,int b,int c)//from a to b,w[a][b]=c;
{
tot++; //边的计数器+1
Next[tot]=one[a]; //先将新边的Next指向one指向的边(防止其丢失),
one[a]=tot; // 再将one指向新边的编号。
ver[tot]=b;
edge[tot]=c;
return;
}
void Init()
{
int i,j;
int a,b,c;
cin>>n>>m;
for(i=1;i<=m;i++) {
scanf("%d%d%d",&a,&b,&c);
AddEdge(a,b,c);//把一个无向边看成两个有向边;
AddEdge(b,a,c);
}
return;
}
遍历方式:
for(int i=one[x];i>0;i=Next[i])
{
y=ver[i]; z=edge[i];
...;
}
这就是链式前向星的全部内容了,还不理解的话,可以再看一遍ヽ(??▽?)ノ;
推荐一篇博客和一部视频
优点
缺点
适用算法
有些算法更关注边而不是点,如最小生成树算法\(kruscal\),和未优化的\(bellman-ford\)算法。
const int N=10000+5;
struct edge
{
int x,y,w; //边的两个端点和边权
};
edge a[N];
void Init()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].w);
return;
}
原文:https://www.cnblogs.com/cjl-world/p/13375953.html