Luogu P2330 [SCOI2005]繁忙的都市

思路

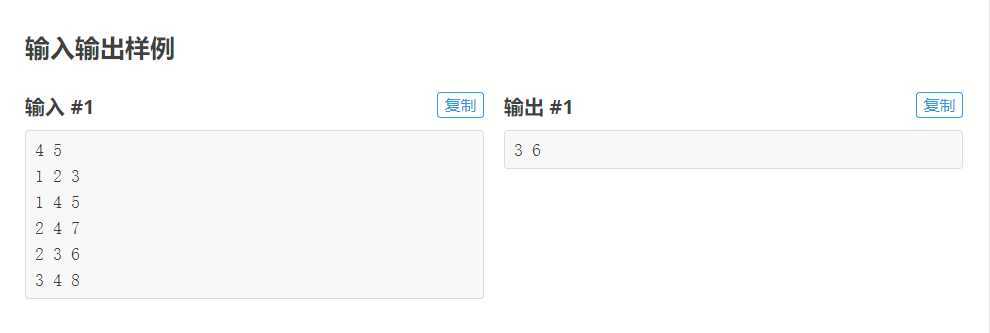
这道题很简单，其实就是一道最小生成树模板题（虽然第一眼可能看成是Floyd）。唯一需要对模板做出的改动就是把模板中的记录最小生成树边权和的操作改为取max即可。这个题看n和m的数据范围其

实Prim比Kruskal更优（Prim更适合稠密图，Kruskal更适合稀疏图），但实际上差不了多少。

Code

//prim
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define MAXN 400
#define MAXM 1000005
#define INF 0x3f3f3f3f
using std::pair;
using std::make_pair;
int n, m, head[MAXN], cnt;
int vis[MAXN], dis[MAXN];
struct node{
    int nxt, to, val;
} edge[MAXM << 1];
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch==‘-‘)f = -1;} while (ch < ‘0‘ || ch > ‘9‘);
    do{ x = x * 10 + ch - ‘0‘;ch = getchar();} while (ch >= ‘0‘ && ch <= ‘9‘);
    return f * x;
}
inline int _max(int x,int y){
    return x > y ? x : y;
}
inline void add_edge(int x,int y,int z){
    ++cnt;
    edge[cnt].nxt = head[x];
    edge[cnt].to = y;
    edge[cnt].val = z;
    head[x] = cnt;
    return;
}
inline void _init(void){
    for (int i = 1; i <= n;++i)
        dis[i] = INF, vis[i] = 0;
    return;
}
int Prim(void){
    std::priority_queue<pair<int, int> > Q;
    int tot = 0, maxx = 0;
    _init();
    dis[1] = 0, Q.push(make_pair(0, 1));
    while(!Q.empty()&&tot<n){
        int d = -(Q.top().first), u = Q.top().second;
        Q.pop();
        if(vis[u]) continue;
        vis[u] = 1;
        ++tot, maxx = _max(maxx, d);//改为求最大值即可
        for (int i = head[u]; i;i=edge[i].nxt){
            int v = edge[i].to;
            if(edge[i].val<dis[v]){
                dis[v] = edge[i].val;
                Q.push(make_pair(-dis[v], v));
            }
        }
    }
    return maxx;
}//模板
int main(){
    n = read(), m = read();
    for (int i = 1; i <= m;++i){
        int u = read(), v = read();
        int w = read();
        add_edge(u, v, w), add_edge(v, u, w);
    }
    printf("%d %d\n", n - 1, Prim());
    return 0;
}

//Kruskal
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define MAXM 100005
#define INF 0x3f3f3f3f
int n, m, cnt;
int f[MAXM << 1], ans;
struct node{
    int from, to, val;
} edge[MAXM << 1];
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch==‘-‘)f = -1;} while (ch < ‘0‘ || ch > ‘9‘);
    do{ x = x * 10 + ch - ‘0‘;ch = getchar();} while (ch >= ‘0‘ && ch <= ‘9‘);
    return f * x;
}
inline int get_father(int k){
    return f[k] == k ? k : f[k] = get_father(f[k]);
}
inline int cmp(const node x,const node y){
    return x.val < y.val;
}
void Kruskal(void){
    for (int i = 1; i <= m;++i){
        int u = get_father(edge[i].from), v = get_father(edge[i].to);
        if(u==v) continue;
        f[u] = v, ans = edge[i].val;//这里由于是从小到大遍历，所以直接存储
        ++cnt;if(cnt==n-1) break;
    }
    return;
}
int main(){
    n = read(), m = read();
    for (int i = 1; i <= m;++i)
        edge[i].from = read(), edge[i].to = read(), edge[i].val = read();
    std::sort(edge + 1, edge + m + 1, cmp);
    for (int i = 1; i <= n;++i)
        f[i] = i;
    Kruskal();
    printf("%d %d\n", n - 1, ans);
    return 0;
}

Luogu P2330 [SCOI2005]繁忙的都市

原文：https://www.cnblogs.com/ShadowFlowhyc/p/13380881.html