Luogu P2894 [USACO08FEB]Hotel G

思路

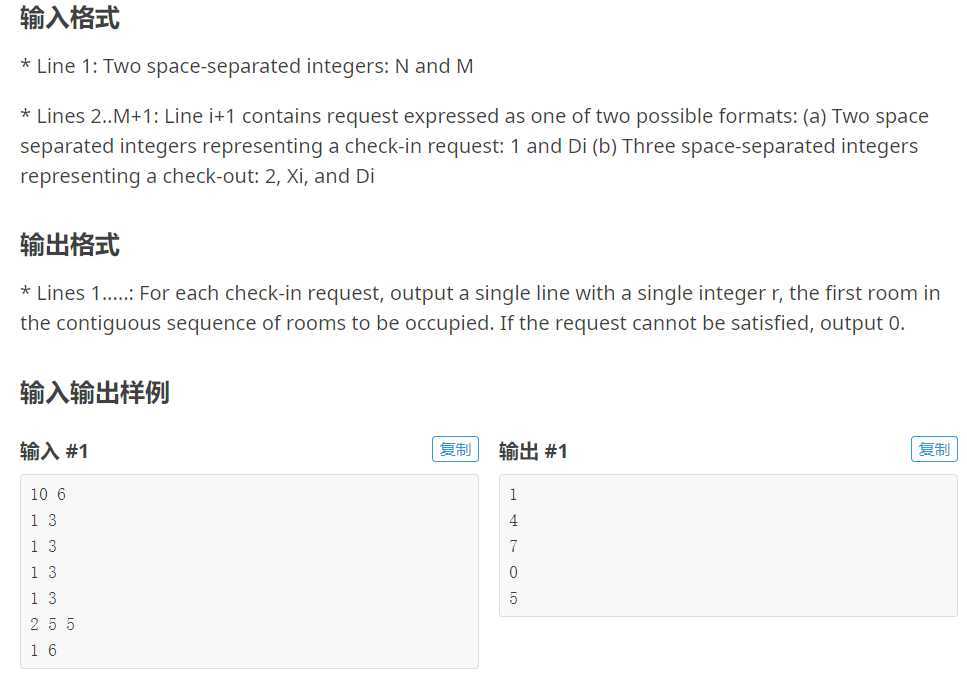
这道题其实说白了也就是一个维护最大连续长度为0的子串，再根据土木中的要求进行更新和求值即可。

我写到这就不知道该怎么说了，所以下面说的可能有些乱。

这道题维护的区间最大子段和GSS1和GSS3的区间最大子段和的维护方法相当的类似，但是由于这道题让你维护的是区间最长的连续为0的子串，而且在查询的时候如果满足了要求，输出的是左端点的序号。

为了维护区间最长连续为0的子串长度，和GSS1、GSS3类似，我们也是要维护区间最大前缀、区间最大后缀和（这里的前缀和和后缀和并不是传统意义上的，维护的东西和区间最长连续空房间是

差不多的），不同的是我们不用维护区间和了，而是要维护区间长度，这也是因为此题维护的是最大区间为0的子串长度。那究竟应该怎么维护呢？

对于区间最长连续为0的子串，它的分布仍然是有3种情况：

1.全部在左儿子

2.全部在右儿子

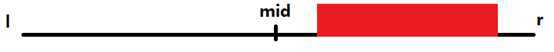
3.在左儿子和右儿子中都有

我们在pushdown的时候，同样也是对这3种情况进行讨论，最后合并取最大值即可。

对于区间最长前缀连续空房间，有两种情况：

1.全部在左儿子中

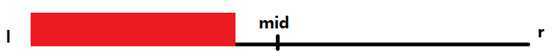
2.在左儿子和右儿子中都有：

同样是在pushdown的时候维护，但是并不是取最大值（因为要连续），而是判断一下左儿子的最大连续空房间数量是不是和左儿子的区长度相同，若相同，那么就是第2种情况，否则就是第一种情况。

对于区间最长后缀连续空房间，其实就是区间最大前缀空房间镜像翻转时候的样子，维护方法极其类似，所以在这里就不再赘述，请大家感性理解一下（因为本人时间有限，没法写的那么详细）。

写到这的时候我感觉有点词穷（我太菜了，不知道该怎么说了），所以就直接看代码好了，主要的东西都写在代码注释里了。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define MAXN 50010
int n, m;
struct node{
    int len;//区间长度
    int val_f, val_b;//最大前缀和最大后缀
    int val_mal;//最长连续空房间
    int tag;//lazytag，0表示还没有操作过，1表示将退房，2表示住上人
} tree[MAXN << 2];
inline int lson(int k) { return k << 1; }//求左儿子
inline int rson(int k) { return k << 1 | 1; }//求右儿子
inline void push_up(int k){
    if(tree[lson(k)].val_mal==tree[lson(k)].len)//若左区间全部为空房，那么就是左区间长度+右区间最大前缀
        tree[k].val_f = tree[lson(k)].len + tree[rson(k)].val_f;
    else//否则直接存储左儿子的最大前缀
        tree[k].val_f = tree[lson(k)].val_f;
    if(tree[rson(k)].len==tree[rson(k)].val_mal)//若右区间全部为空房，那么就是右区间长度+左区间最大前缀
        tree[k].val_b = tree[rson(k)].len + tree[lson(k)].val_b;
    else//否则直接存储右儿子最大后缀
        tree[k].val_b = tree[rson(k)].val_b;
    tree[k].val_mal = std::max(std::max(tree[lson(k)].val_mal, tree[rson(k)].val_mal), tree[lson(k)].val_b + tree[rson(k)].val_f);
    return;//对所有可能的最大连续空房间的长度取max
}
inline void push_down(int k,int l,int r){
    if(tree[k].tag==0)
        return;//若没有操作，直接返回
    if(tree[k].tag==1){//若将这个区间全部退房，那么这个区间的所有值都为区间长度
        tree[lson(k)].tag = 1;
        tree[rson(k)].tag = 1;
        tree[lson(k)].val_mal = tree[lson(k)].len;
        tree[rson(k)].val_mal = tree[rson(k)].len;
        tree[lson(k)].val_f = tree[lson(k)].len;
        tree[rson(k)].val_f = tree[rson(k)].len;
        tree[lson(k)].val_b = tree[lson(k)].len;
        tree[rson(k)].val_b = tree[rson(k)].len;
    }
    if(tree[k].tag==2){//同上，若全部住上人，那么所有值都设为0
        tree[lson(k)].tag = 2;
        tree[rson(k)].tag = 2;
        tree[lson(k)].val_mal = 0;
        tree[rson(k)].val_mal = 0;
        tree[lson(k)].val_f = 0;
        tree[rson(k)].val_f = 0;
        tree[lson(k)].val_b = 0;
        tree[rson(k)].val_b = 0;
    }
    tree[k].tag = 0;//清空标记
    return;
}
void build(int k,int l,int r){
    tree[k].tag = 0;
    tree[k].val_mal = r - l + 1;
    tree[k].val_f = r - l + 1;
    tree[k].val_b = r - l + 1;
    tree[k].len = r - l + 1;//一开始所有的房间均为空
    if(l==r)
        return;
    int mid = (l + r) >> 1;
    build(lson(k), l, mid);
    build(rson(k), mid + 1, r);
    push_up(k);
}
void update(int k,int cl,int cr,int l,int r,int v){
    if(cl<=l&&r<=cr){
        tree[k].tag = v;//若当前区间完全被包含在修改区间中，直接修改，更新lazytag
        if(v==1){
            tree[k].val_f = tree[k].len;
            tree[k].val_b = tree[k].len;
            tree[k].val_mal = tree[k].len;
        }
        if(v==2){
            tree[k].val_f = 0;
            tree[k].val_b = 0;
            tree[k].val_mal = 0;
        }
        return;
    }
    push_down(k, l, r);
    int mid = (l + r) >> 1;
    if(cl<=mid)//基础线段树操作
        update(lson(k), cl, cr, l, mid, v);
    if(cr>mid)
        update(rson(k), cl, cr, mid + 1, r, v);
    push_up(k);
}
int query(int k,int qlen,int l,int r){
    push_down(k, l, r);
    if(l==r)
        return l;
    int mid = (l + r) >> 1;
    if(tree[lson(k)].val_mal>=qlen)//由于题目要找的是最左边的端点，所以尽量往左找
        return query(lson(k), qlen, l, mid);
    else if(tree[lson(k)].val_b+tree[rson(k)].val_f>=qlen)
        return mid - tree[lson(k)].val_b + 1;//返回区间长度
    else//在左边实在是找不到再往右找
        return query(rson(k), qlen, mid + 1, r);
}
int main(){
    scanf("%d%d", &n, &m);
    build(1, 1, n);//建树……
    for (int i = 1; i <= m;++i){
        int opt = 0;
        scanf("%d", &opt);
        if(opt==1){
            int x = 0, ls = 0;
            scanf("%d", &x);
            if(tree[1].val_mal>=x){
                ls = query(1, x, 1, n);
                printf("%d\n", ls);
                update(1, ls, ls + x - 1, 1, n, 2);
                //这里如果找到不要忘记更新！
            }
            else
                puts("0");
        }
        if(opt==2){
            int l = 0, r = 0;
            scanf("%d%d", &l, &r);
            update(1, l, l + r - 1, 1, n, 1);
            //这里注意操作区间是l~l+r-1，而不是l~r
        }
    }
    return 0;
}

Luogu P2894 [USACO08FEB]Hotel G

原文：https://www.cnblogs.com/ShadowFlowhyc/p/13380930.html