Luogu P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

思路

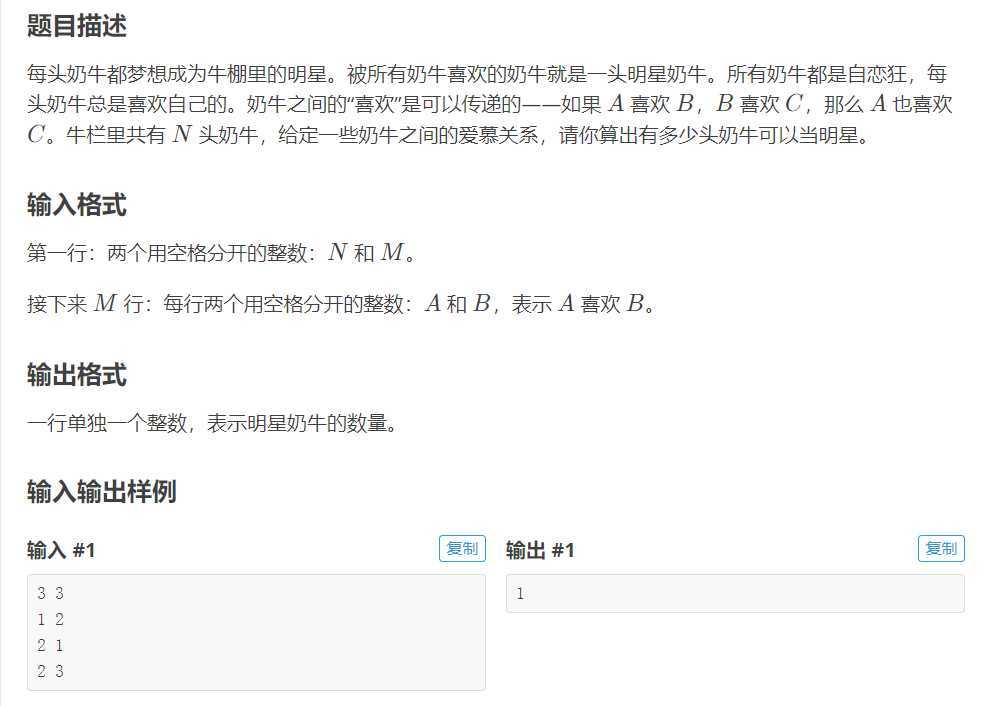
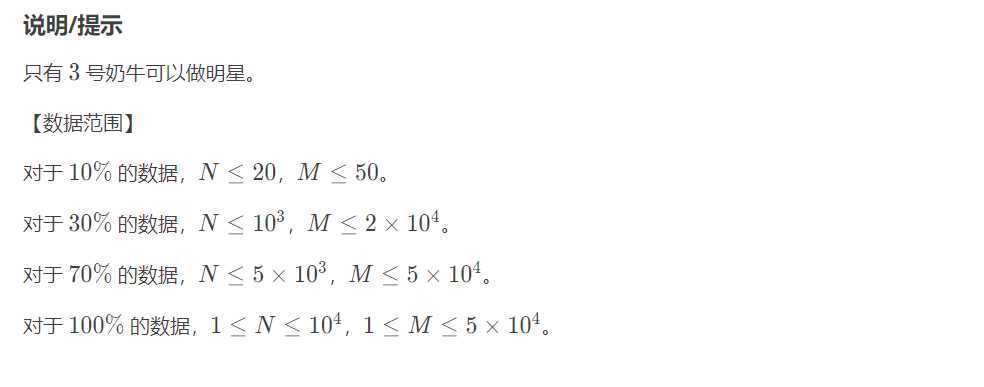
如果 A 认为 B 受欢迎，A 向 B 连边。 Tarjan 求强连通分量缩点后的图，出度为 0 的点若只有?个则 输出其代表的强连通分量的??，否则?解。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define MAXN 10005
#define MAXM 50005
int n, m, idx, scc;
int head[MAXN], cnt;
int dfn[MAXN], low[MAXN];
int bel[MAXN], col[MAXN];
int out[MAXN];
bool flag[MAXN];
class node{
    public: int nxt, to;
} edge[MAXM];
class Stack{
    private:
        int stk[MAXN], top;
    public:
        inline void Push(int x) { stk[++top] = x; return; }
        inline void Pop(void) { --top; return; }
        inline int Top(void) { return stk[top]; }
} Stk;
inline int read(void){
    int f = 1, x = 0;char ch;
    do{ch = getchar();if(ch==‘-‘)f = -1;} while (ch < ‘0‘ || ch > ‘9‘);
    do{ x = (x << 1) + (x << 3) + ch - ‘0‘;ch = getchar();} while (ch >= ‘0‘ && ch <= ‘9‘);
    return f * x;
}
inline int _min(int x, int y) { return x < y ? x : y; }
inline void add_edge(int x,int y){
    ++cnt;
    edge[cnt].nxt = head[x];
    edge[cnt].to = y;
    head[x] = cnt;
    return;
}
void tarjan(int k){
    dfn[k] = low[k] = ++idx;
    Stk.Push(k);
    flag[k] = 1;
    for (int i = head[k]; i; i=edge[i].nxt){
        int v = edge[i].to;
        if(!dfn[v])
            tarjan(v),low[k] = _min(low[k], low[v]);
        else if(flag[v])low[k] = _min(low[k], dfn[v]);
    }
    int now = -1;
    if(dfn[k]==low[k]){
        ++scc;
        while(now!=k){
            now = Stk.Top();Stk.Pop();
            flag[now] = 0;
            bel[now] = scc;
            ++col[scc];
        }
    }
}
int main(){
    n = read(), m = read();
    for (int i = 1; i <= m;++i){
        int u = read(), v = read();
        add_edge(u, v);
    }
    for (int i = 1; i <= n;++i)
        if(!dfn[i]) tarjan(i);
    for (int i = 1; i <= n;++i){
        for (int j = head[i]; j;j=edge[j].nxt){
            int v = edge[j].to;
            if(bel[i]!=bel[v]) ++out[bel[i]];
        }
    }
    for (int i = 1; i <= n;++i)
        printf("%d %d\n", dfn[i], low[i]);
    int res = 0;
    for (int i = 1; i <= scc;++i){
        if(!out[i]){
            if(res) { puts("0"); return 0; }
            res = i;
        }
    }
    printf("%d\n", col[res]);
    return 0;
}

Luogu P2341 [USACO03FALL][HAOI2006]受欢迎的牛 G

原文：https://www.cnblogs.com/ShadowFlowhyc/p/13380893.html