
树状数组,顾名思义,就是要把一个数组的存储形式抽象成一棵树的形式,来高效地完成一些在数组中的操作。那么树状数组的原理是什么呢?我们可以尝试将数组下标(假设从1开始编号)转化成二进
制数,则1,2,3,4,5,6,7,8分别对应着二进制的1,10,11,100,101,110,111,1000。然后我们可以艰难地发现一个有趣的性质,那就是如果我们把一个二进制数的第一个1和这个1后面的0一起提取出来,
再将这个数加上提取出来的这个数,又可以得到一个新的数。例如6的二进制是110,我们把它的第一个1和后面的0提取出来为10,对应十进制为2,6+2等于8,我们就得到了8这个数,也就可以完成一次
更新。利用这个性质,我们可以画出这样的一幅图(图采集自百度百科):
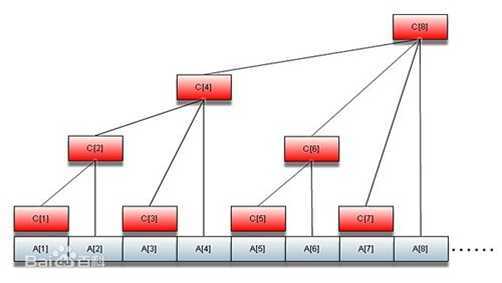
由此我们可以总结出:
C1=A1
C2=A1=A2
C3=A3
C4=A1+A2+A3+A4
C5=A5
C6=A5+A6
C7=A7
C8=A1+A2+A3+A4+A5+A6+A7+A8
C1=A1
C2=C1+A2
C3=A3
C4=C2+C3+A4
C5=A5
C6=C5+A6
C7=A7
C8=C4+C6+C8+A8
那么,我们该如何实现C数组的各个元素之间的相互关联呢?这时我们的lowbit就横空出世出现了。
在前面的介绍中讲到,我们将数组下标转化为二进制之后将二进制数的第一个1及其后面的0给揪出来,再把这个数加上这个被揪出来的二进制数,就可以完成图中的转化。那么我们怎么计算第一个1的位置呢?
现在举一个例子。比如说6这个数,它的二进制为110,那么它的原码(一个整数按照绝对值大小转换成的二进制数,是为原码。)就是在它的二进制前面补上6个0,即为000000110,它的反码就是将它
的原码取反,即为111111001。然后将反码加1,得到补码(反码加1叫做补码),即为111111010,而补码就是负数在计算机中的表示形式。然后我们将000000110和111111010这两个数做按位与
(在C++中表示为“&”,在对两个二进制数做按位与运算时,结果为这两个二进制数的每一位取最小值)运算,就可以得到6在二进制下的第一个1和它后面的0所表示的数为10,即为2。6+2=8,就完成了
从6到8的更新。这也就是lowbit的计算方法: x&(-x)。
有了lowbit之后,我们就可以轻松地完成树状数组的更新和查询。树状数组模板1要求我们完成的是单点修改和区间查询。对于单点修改,我们不仅仅要更改他所需要改的那个点,还需要同时更新树状
数组中与他关联的所有点。这就需要用lowbit来遍历每一个更改改点后所影响的点,并进行更新。对于区间查询,我们要利用差分的思想,若查询区间l到r中每个数的和,那么我们就可以查询从1—r的
和(记为u)从1—l-1的和(记为v),则u-v即为l—r区间内每个数的和。之所以这样做,是因为树状数组的特性导致只能用树状数组求1—x的和。而不能直接求任意一个区间的和。求1—x的和与单点修
改类似,我们从x开始,每次累加答案,并将x-=lowbit(x),就可以求出1-x这个区间内每个数的和了。
Code
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<queue>
#include<map>
#define MAXN 500005
#define lowbit(x) x&(-x)
typedef long long ll;
int n,m,tree[MAXN];
inline void Insert(int x,int k){
for(;x<=n;x+=lowbit(x))
tree[x]+=k;
return;
}
inline ll Query(int x){
ll res=0;
for(;x>=1;x-=lowbit(x))
res+=tree[x];
return res;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i){
int k=0;
scanf("%d",&k);
Insert(i,k);
}
for(int i=1;i<=m;++i){
int opt,x,y;
scanf("%d",&opt);
scanf("%d%d",&x,&y);
if(opt==1)Insert(x,y);
if(opt==2)
printf("%lld\n",Query(y)-Query(x-1));
}
return 0;
}
原文:https://www.cnblogs.com/ShadowFlowhyc/p/13381822.html