从0开始的机器学习——梯度下降法（3）

在解决问题中，θ可能不是一个值，可能是一个向量，所以在求导的时候可以写成求梯度的形式，求函数在每个方向上的偏导数。

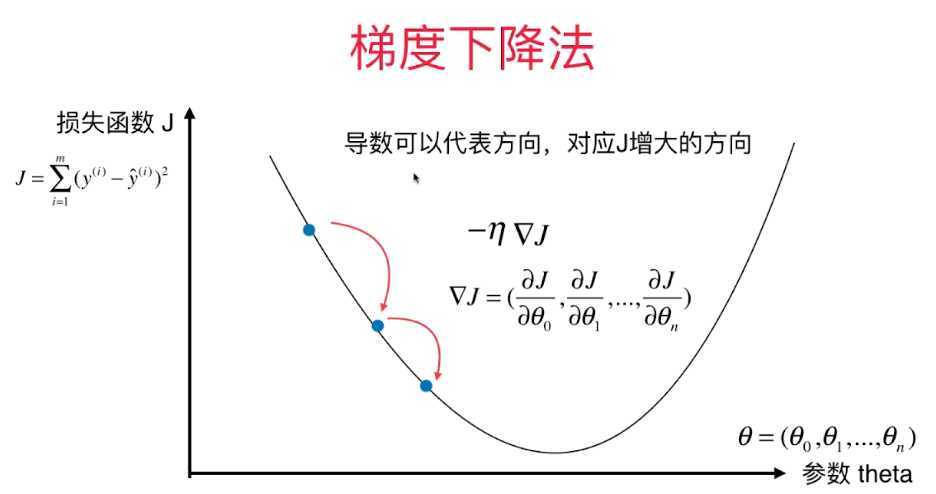
其实和上一节处理的问题也相似，只不过这个处理的不是一个数，是一个向量。

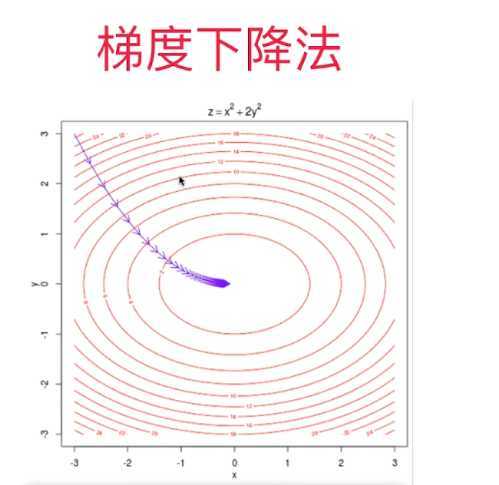
这是一个三元函数的曲线图。图中的红色圈圈就是函数曲线。假如起始点从左上角那个点出发，一直到数值最低的点，其实这个路径选择有无数条，但是我们要找的就是下降速度最快的那个。

下面看梯度下降法的目标：

但是这样的向量有一个弊端：因为m的值可能会很大，可能导致向量的值很大，在计算中出现问题。所以要对最后的向量形式进行改进，比如在外面乘1/m，减少m对向量的影响。

有时候取外面乘1/2的，和向量外面的2约去，但是一个常数影响是很小的，也可以不约去2。

代码实现：

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = 2 * np.random.random(size=100)  #100个只有一个特征的数据点
y = x * 3. + 4. + np.random.normal(size=100)

X = x.reshape(-1,1)

plt.scatter(x,y)
plt.show()

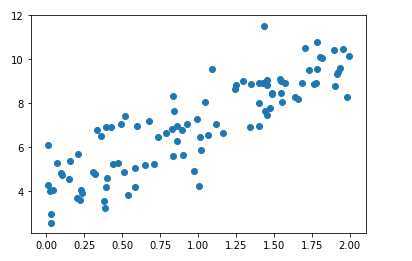
得到这样的散点图

def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)
    except:
        return float(‘inf‘)
   

def dJ(theta, X_b, y):
    res = np.empty(len(theta))
    res[0] = np.sum(X_b.dot(theta) - y)
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta) - y).dot(X_b[:,i])
    return res * 2 / len(X_b)

def gradient_descent(X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    
    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
            
        cur_iter += 1

    return theta

X_b = np.hstack([np.ones((len(x), 1)), x.reshape(-1,1)])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

theta = gradient_descent(X_b, y, initial_theta, eta)

获得斜率和截距，和最开始动手设置的基本吻合，证明梯度下降是成功的。

从0开始的机器学习——梯度下降法（3）

原文：https://www.cnblogs.com/xiyoushumu/p/13386992.html