
先计算从low到high一共有多少个数: int diff = high - low + 1;
找规律发现,如果low和high都是奇数,那么奇数个数就是diff上取整,其他情况奇数数目都是diff下取整。
class Solution {
public:
int countOdds(int low, int high) {
int diff = high - low + 1;
if(low % 2 == 1 && high % 2 == 1) {
return diff / 2 + 1;
}
return diff / 2;
}
};

看到子数组自然会想到用前缀和来处理,如果用一个二维数组来记录某个位置到另一个位置的子数组和,则时间复杂度为O(n^2),超时。
这题只需要求子数组是奇数的数目,不需要给出具体的子数组,因此不需要开二维数组,可以用两个变量odd和even记录当前位置之前的所有子数组的
和为奇数和偶数的数目,这样遍历到当前元素时,我们只需要求出从数组开头到当前元素的所有元素的元素和(即到当前元素的子数组的和)是奇数还是偶数。
如果是偶数,则答案加上odd,因为odd表示之前的和为奇数的子数组的数目,从某个和为奇数的子数组的末尾元素的下一个位置开始到当前元素的子数组的和为奇数。
如果是奇数,则答案加上even,因为even表示之前的和为偶数的子数组的数目,从某个和为偶数的子数组的末尾元素的下一个位置开始到当前元素的子数组的和为奇数。
这样只需要一遍遍历数组就可以了,时间复杂度是O(n)。
class Solution {
public:
int numOfSubarrays(vector<int>& arr) {
int mod = 1e9 + 7;
int res = 0, sum = 0, odd = 0, even = 1; //res表示最终答案,sum记录从数组开头到当前元素的子数组的和,odd表示当前元素之前的子数组和为奇数的数目,even表示当前元素之前的子数组和为偶数的数目
for(auto x : arr) {
sum += x;
if(sum % 2 == 1) { //如果从数组元素到当前元素的子数组的和为奇数
res = (res + even) % mod; //则答案加上even
++odd;
} else {
res = (res + odd) % mod;
++even;
}
}
return res;
}
};
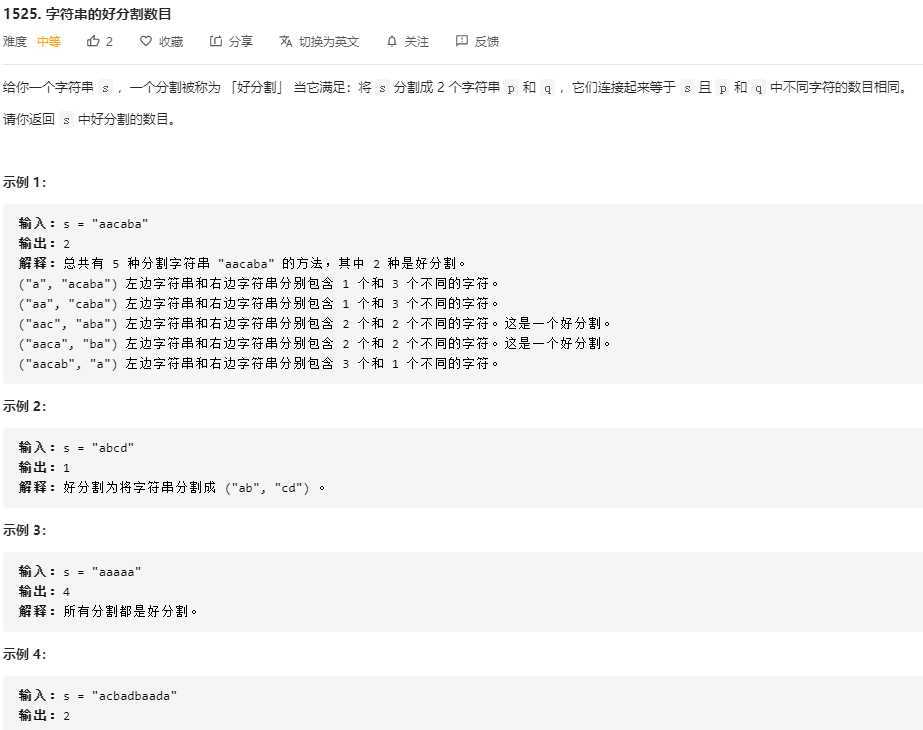
暴力:遍历一下字符串,对于每个可以分割的位置,划分出左右子串,然后统计左右子串不同元素的个数,再进行笔记。
这样时间复杂度是O(n^2),超时。
超时的主要原因是划分子串之后对于子串还要进行遍历来计算不同元素的个数,所以如果对于每一个分割点,可以短时间内计算出左右子串中不同元素的个数,就可以
把时间复杂度控制在O(n)。
可以用两个数组left和right实时记录左右子串中各个字符的出现次数,再用两个变量countLeft和countRight记录实时的左右子串中不同字符的数目。
然后初始时(可以认为分割点在第一个字符之前),计算出s中所有字符的出现次数,记录到right数组,也就是相当于分割出来的左子串为空,右子串就是S。
然后从左向右枚举分割点,对于每个分割点,左子串都增加了一个字符,看一下left数组中这个字符是否为0,如果为0,表示左子串多了一个未出现的字符,countLeft加一;对于每个分隔点,右子串都减小了一个字符,看一下right数组中这个字符减一是否为0,如果为0,说明右子串少了一个(子串其他部分没有的)字符,countRight减一。
每个分割点计算出来的countLeft和countRight都要进行比较,如果相等,则答案加一。
代码如下:
class Solution {
public:
void changeLeft(vector<int>& left, int& countLeft, int c) { //分割点向左移动时,看一下左子串的不同字符个数countLeft是否有增加。 注意这里left数组和countLeft都是引用类型
if(left[c] == 0) { //如果原来的左子串没有这个字符
++countLeft; //说明左子串字符总类数加一
}
++left[c]; //left数组和right数组都是对每个字符的出现次数做哈希,c是字符与‘a‘的偏移量
}
void changeRight(vector<int>& right, int& countRight, int c) { //分割点向右移动时,看一下右子串的不同字符个数countRight是否减小。
--right[c]; //分割点的这个字符的出现次数减一
if(right[c] == 0) { //出现次数减到0,说明右子串的字符总类个数减一
--countRight;
}
}
int numSplits(string s) {
int res = 0;
int countLeft = 0, countRight = 0; //左、右子串不同字符的个数
vector<int> left(26, 0), right(26, 0); //对于左右子串不同的字符出现次数做哈希
for(auto ch : s) {
int c = ch - ‘a‘; //c是字符与‘a‘的偏移量
countRight += (right[c] == 0 ? 1 : 0); //最开始认为分割点在s第一个字符之前,即左子串为空,右子串为s,这时countRight就是s中不同字符的种类个数
++right[c]; //当前字符的出现次数加一
}
for(int i = 0; i < s.size() - 1; ++i) { //枚举分割点,即将当前字符s[i]从右子串删除,加入左子串
int c = s[i] - ‘a‘;
changeLeft(left, countLeft, c);
changeRight(right, countRight, c);
if(countLeft == countRight) {
++res;
}
}
return res;
}
};
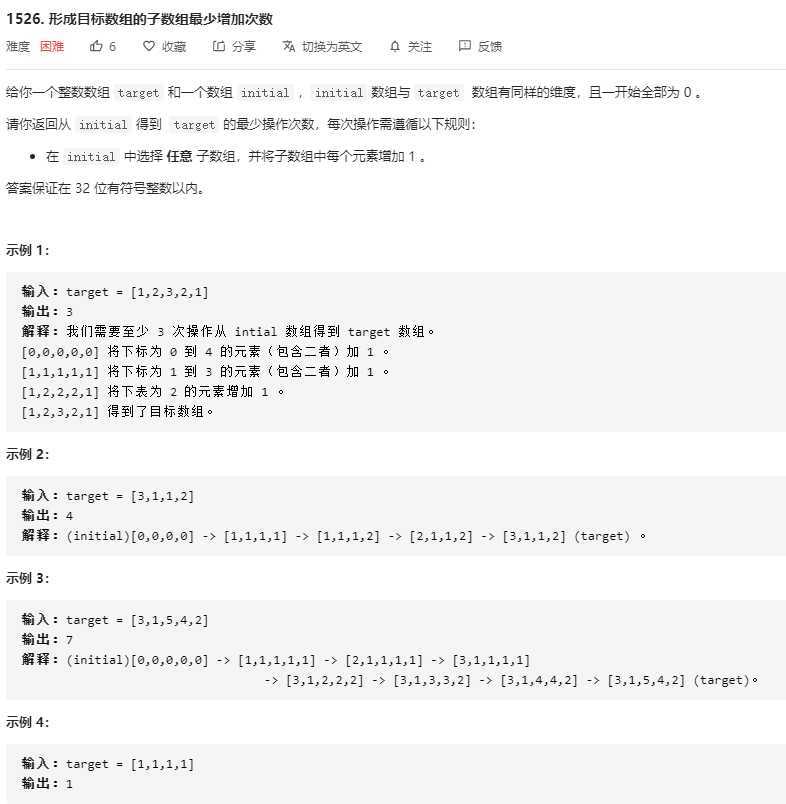
初始时,肯定最少需要target[0]次累加使第一个位置符合要求,不过累加了target[0]次也使得后面的部分位置满足要求。
遍历数组,考虑相邻两个位置的差值target[i] - target[i - 1],如果target[i] - target[i - 1] > 0, 则最少还需要target[i] - target[i - 1]次操作才能使第i个位置满足要求,否则,我们可以认为target[i]已经被之前的操作填充满了。
class Solution {
public:
int minNumberOperations(vector<int>& target) {
int res = target[0];
for(int i = 1; i < target.size(); ++i) {
res += max(0, target[i] - target[i - 1]);
}
return res;
}
};
原文:https://www.cnblogs.com/linrj/p/13392169.html