题目

题目

做法

题目很明显是问你编号为\(i\)的坐标，然后用勾股定理。

其实不难看出一个事情，就是你可以把第二幅图看成第一幅图，然后按一=》二的方法去变成二=》三。

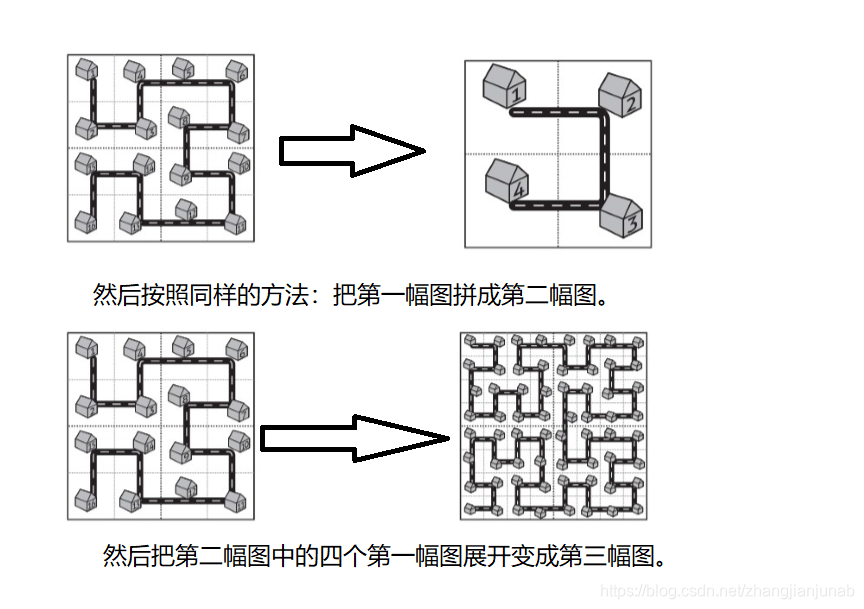
所以不难看出的是所有等级的图都可以堪称\(n=1\)的图然后拼成\(n=2\)的图等量代换。

所以我们可以找到规律，拼图的顺序是（‘.‘号是用来占位置的，与题目无关，-|才有关）：
1-2
....|
4-3

所以，对于一个正方形，我们可以把四个部分分别DFS，但是这样还是太复杂了，我们需要找到四个部分的关系。

这能有什么关系，乱七八糟的，但是我们上面都说了，是由同一种图形拼成的，也就是说四个部分之间可能只是旋转和翻折的的区别。

这里我说一下，2、3部分相等，1是2左右翻折再加顺时针旋转90°，而\(4\)是\(1\)旋转180°得到的矩阵，所以我们就可以通过这个关系把四个部分的DFS合为一个DFS，然后把坐标的乘以他们之间的关系就行了。

对于一个点，看看他在四个部分的哪个部分，然后又DFS一层，继续看他在哪个部分，继续DFS，直到到底（即等级1）为止就可以求出这个点的坐标了。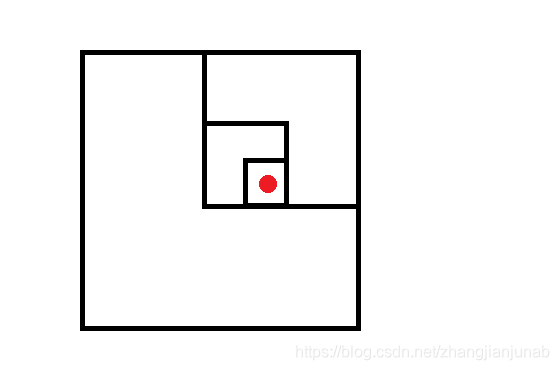

至于旋转坐标变化的公式，我就不说了，推荐你拿一张纸，然后画个矩阵，然后像我这样标出来，把纸转一下，就很明了了。

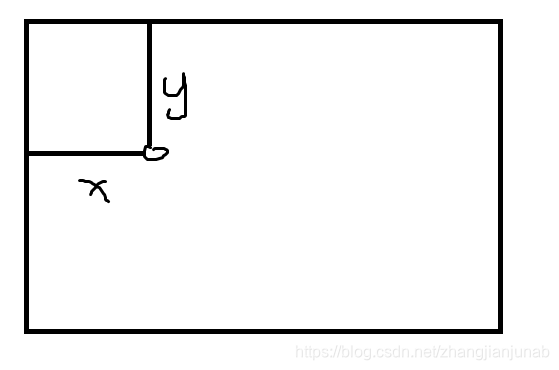
时间复杂度：\(O(nN)\)

代码

注：这里的坐标是这样的：

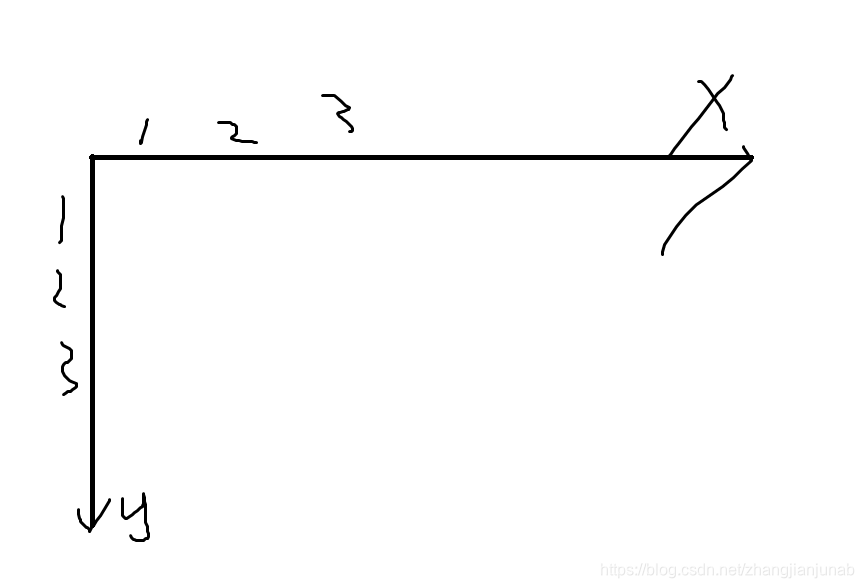
#include<cstdio>
#include<cstring>
#include<cmath>
using  namespace  std;
typedef  long  long  LL;
struct  node
{
	LL  x,y;
};
inline  node  make(LL  x,LL  y){node  t;t.x=x;t.y=y;return  t;}
inline  node  f1(node  x,LL  n/*每个块的边长*/)/*以第标准块的视角来看第一个块*/
{
	return  make(x.y/*n-(n-y+1)+1*/,x.x);
}
inline  node  f2(node  x,LL  n){return  make(x.x+n,x.y);}//第二三个块其实就是标准块来着。
inline  node  f3(node  x,LL  n){return  make(x.x+n,x.y+n);}
inline  node  f4(node  x,LL  n){return  make(n-x.y+1,n-x.x+1+n);}
//对于每一个块的处理
inline  node  fuck(LL  id)
{
	if(id<=2)return  make(id,1);
	else  return  make(4-id+1,2);
}
LL  f[100];//f[n]表示n等级时的边长 
node  dfs(LL  id,int  n/*等级*/)//得到编号的坐标 
{
	if(n==1)return  fuck(id);
	int  m=n-1;
	if(id<=2*f[m]*f[m])
	{
		if(id<=f[m]*f[m])return  f1(dfs(id,m),f[m]);
		else  return  f2(dfs(id-f[m]*f[m],m),f[m]);
	}
	else
	{
		if(id<=3*f[m]*f[m])return  f3(dfs(id-2*f[m]*f[m],m),f[m]);
		else  return  f4(dfs(id-3*f[m]*f[m],m),f[m]);
	}
}
int  main()
{
	int  T;scanf("%d",&T);
	f[0]=1;for(int  i=1;i<=31;i++)f[i]=f[i-1]*2;
	while(T--)
	{
		int  n;LL  A,B;scanf("%d%lld%lld",&n,&A,&B);
		node  a=dfs(A,n),b=dfs(B,n);
		double  x=sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
		printf("%.0lf\n",x*10);
	}
	return  0;
}

分形之城

原文：https://www.cnblogs.com/zhangjianjunab/p/13395236.html