相关方法

已知p,q,e求d

1. 方法一：

p=473398607161
q=4511491
e=17
n = (p-1) * (q-1)

def extendedEuclid(a, b):
    if b == 0:
        return 1, 0
    else:
        x, y= extendedEuclid(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y
d = extendedEuclid(e,n)[0]
print(d)

2. 方法二(常用，gmpy2库)：

# 已知e,p,q
import gmpy2
phin = (p-1) * (q-1)
d = gmpy2.invert(e,phin)

3. 方法三(sage)：

phin = (p-1) * (q-1)
d = inverse_mod(e,phin)

例题

Buuoj RSA

1. 给了flag.enc和pub.key文件，其中pub.key文件存放了公钥信息，这是个ASCII文本文件可直接用记事本打开。得到以下信息：

-----BEGIN PUBLIC KEY-----
MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9+7+
/AvKr1rzQczdAgMBAAE=
-----END PUBLIC KEY-----

2. 借助RSA密钥解析网站解析密钥指数和模数信息，得以下结果：

key长度：256
模数：C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
指数：65537

3. 用Python得到n的十进制形式

n = ‘0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD‘
n = int(n,16)

4. 得到n=86934482296048119190666062003494800588905656017203025617216654058378322103517，放到大数分解网站分解。得到：

p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463

5. 利用gmpy2库求解d，由以上已得数据有以下代码d = gmpy2.invert(e,(p-1)*(q-1))，得到：

d=81176168860169991027846870170527607562179635470395365333547868786951080991441

注意这个invert函数的用法：

invert(x, m) Return y such that x*y == 1 (mod m).

6. 最后从flag.enc文件中获取flag

import rsa
k = rsa.PrivateKey(n,e,int(d),p,q)
f = open("flag.enc","rb+").read()
flag = rsa.decrypt(f,k)
print(flag)

flag{decrypt_256}

注意这个rsa.PrivateKey所有的参数都要是int

BJDCTF 2nd rsa0

1. 给了node3.buuoj.cn:29594，nc连接，得到
   

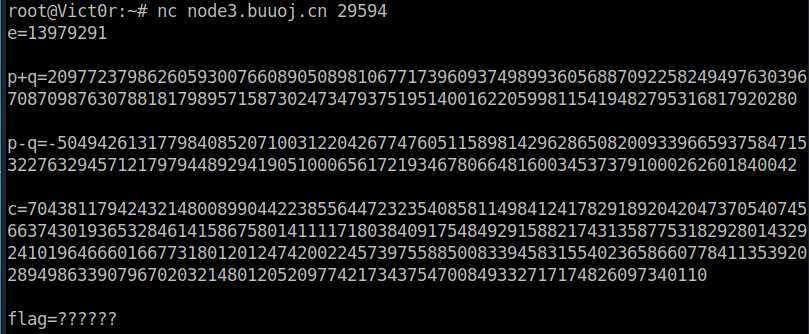
e = 13979291
p+q = 20977237986260593007660890508981067717396093749899360568870922582494976303967087098763078818179895715873024734793751951400162205998115419482795316817920280
p-q = -5049426131779840852071003122042677476051158981429628650820093396659375847153227632945712179794489294190510006561721934678066481600345373791000262601840042
c = 70438117942432148008990442238556447232354085811498412417829189204204737054074566374301936532846141586758014111171803840917548492915882174313587753182928014329241019646660166773180120124742002245739755885008339458315540236586607784113539202894986339079670203214801205209774217343754700849332717174826097340110

2. Python代码如下：

import gmpy2
from Crypto.Util.number import long_to_bytes

p_add_q = 20977237986260593007660890508981067717396093749899360568870922582494976303967087098763078818179895715873024734793751951400162205998115419482795316817920280
p_sub_q = -5049426131779840852071003122042677476051158981429628650820093396659375847153227632945712179794489294190510006561721934678066481600345373791000262601840042
c = 70438117942432148008990442238556447232354085811498412417829189204204737054074566374301936532846141586758014111171803840917548492915882174313587753182928014329241019646660166773180120124742002245739755885008339458315540236586607784113539202894986339079670203214801205209774217343754700849332717174826097340110
p = (p_add_q + p_sub_q)//2
q = (p_add_q - p_sub_q)//2
phn = (p - 1) * (q - 1)
e = 13979291
d = gmpy2.invert(e,phn)
n = p * q
m = pow(c,int(d),n)
print(long_to_bytes(m))

flag{2824f2c0-b958-4d96-9ce7-1b3d40e9333d}

BJDCTF 2nd rsa1

1. nc node3.buuoj.cn 28900得到：
   

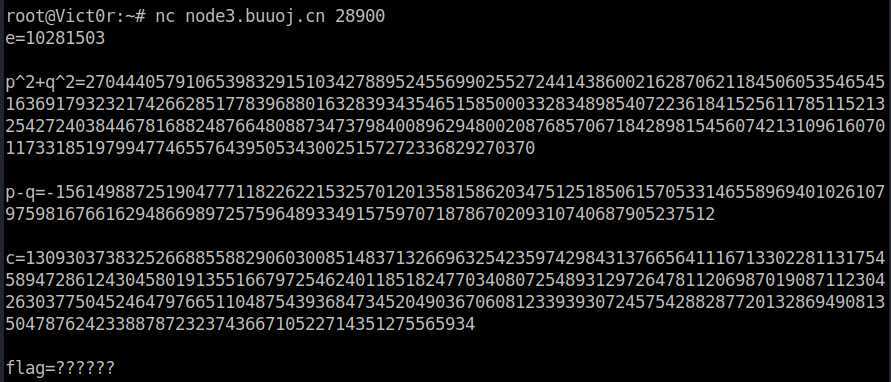
e = 10281503
p^2 + q^2 = 270444057910653983291510342788952455699025527244143860021628706211845060535465451636917932321742662851778396880163283934354651585000332834898540722361841525611785115213254272403844678168824876648088734737984008962948002087685706718428981545607421310961607011733185197994774655764395053430025157272336829270370
p - q=-1561498872519047771182262215325701201358158620347512518506157053314655896940102610797598167661629486698972575964893349157597071878670209310740687905237512
c = 130930373832526688558829060300851483713266963254235974298431376656411167133022811317545894728612430458019135516679725462401185182477034080725489312972647811206987019087112304263037750452464797665110487543936847345204903670608123393930724575428828772013286949081350478762423388787232374366710522714351275565934

2. 根据pq的信息解方程即可，2(p^2 + q^2) - (p-q)^2 = (p+q)^2，emmm想用Python的cmath开根号或pow时会报溢出，所以整个解题过程在sage中实现。
3. sage代码如下：

import binascii
x = 270444057910653983291510342788952455699025527244143860021628706211845060535465451636917932321742662851778396880163283934354651585000332834898540722361841525611785115213254272403844678168824876648088734737984008962948002087685706718428981545607421310961607011733185197994774655764395053430025157272336829270370
p_sub_q = -1561498872519047771182262215325701201358158620347512518506157053314655896940102610797598167661629486698972575964893349157597071878670209310740687905237512
p_add_q = sqrt(2*x-pow(p_sub_q,2))
p = (p_add_q + p_sub_q)//2
q = (p_add_q - p_sub_q)//2
phn = (p - 1) * (q - 1)
e = 10281503
d = inverse_mod(e,phn)
n = p * q
c = 130930373832526688558829060300851483713266963254235974298431376656411167133022811317545894728612430458019135516679725462401185182477034080725489312972647811206987019087112304263037750452464797665110487543936847345204903670608123393930724575428828772013286949081350478762423388787232374366710522714351275565934
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:]))

flag{795faee7-4d4b-432c-9796-4758027c8a58}

Reference

https://baike.baidu.com/item/扩展欧几里得算法/2029414?fr=aladdin

RSA

原文：https://www.cnblogs.com/vict0r/p/13192535.html