探究|等面积法及其应用

前言

典例剖析

(1).[初中]如图所示，直线\(m//n\)，点\(A\)，\(B\)，\(C\)是定点，点\(D\)为直线\(m\)上的动点，则\(S_{\triangle ABC}=S_{\triangle ABD}\).

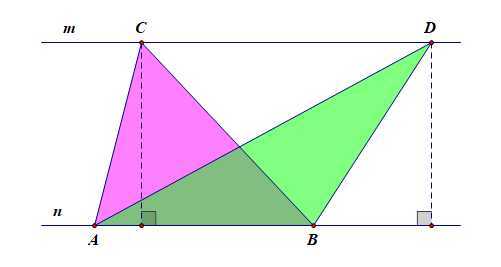
理由：同底等高；两平行线间的距离相等；

(2).[初中探究]如图所示的多边形\(ABCDE\)，若想过点\(E\)作一条直线\(EF\)(其中点\(F\)位于直线\(BC\)上)，使得直线\(EF\)左侧的四边形\(ABFE\)面积和多边形\(ABCDE\)的面积相等，请写出设计方案，并说明理由。

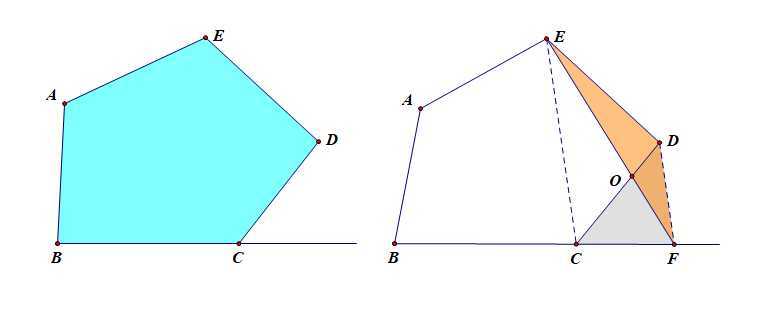
做法：连结\(EC\)，过点\(D\)做\(DF//EC\)交\(BC\)于\(F\)，连结\(EF\)，则直线\(EF\)为所求；

说明：由于\(S_{多边形ABCDE}=S_{多边形ABCOE}+S_{\triangle EOD}\)，\(S_{四边形ABFE}=S_{多边形ABCOE}+S_{\triangle COF}\)，

又由于\(EC//DF\)，由同底等高的缘故可知，\(S_{\triangle DFE}=S_{\triangle DFC}\)，

又由于\(S_{\triangle DFE}=S_{\triangle DFO}+S_{\triangle DOE}\)，\(S_{\triangle DFC}=S_{\triangle DFO}+S_{\triangle COF}\)，

故\(S_{\triangle DOE}=S_{\triangle COF}\)，故\(S_{多边形ABCDE}=S_{四边形ABFE}\)，

即直线\(EF\)为符合题意的直线。

探究|等面积法及其应用

原文：https://www.cnblogs.com/wanghai0666/p/13398459.html