这篇博客提供一种理解KMP算法中求解next数组的思路,若是从头开始学习KMP算法,请移步这篇博客阅,作者讲解的十分详细,我本人也是从他的博客开始回顾KMP算法,本篇博客也是基于这篇博客来写的。
请阅读到以下位置后,若是无法理解P[k] != P[j]这部分逻辑,希望可以尝试用本篇博客的思路来理解;若是理解了,这篇博客也可以帮你以另外一种思路理解,所以本篇博客作为这篇博客的补充更为合适。
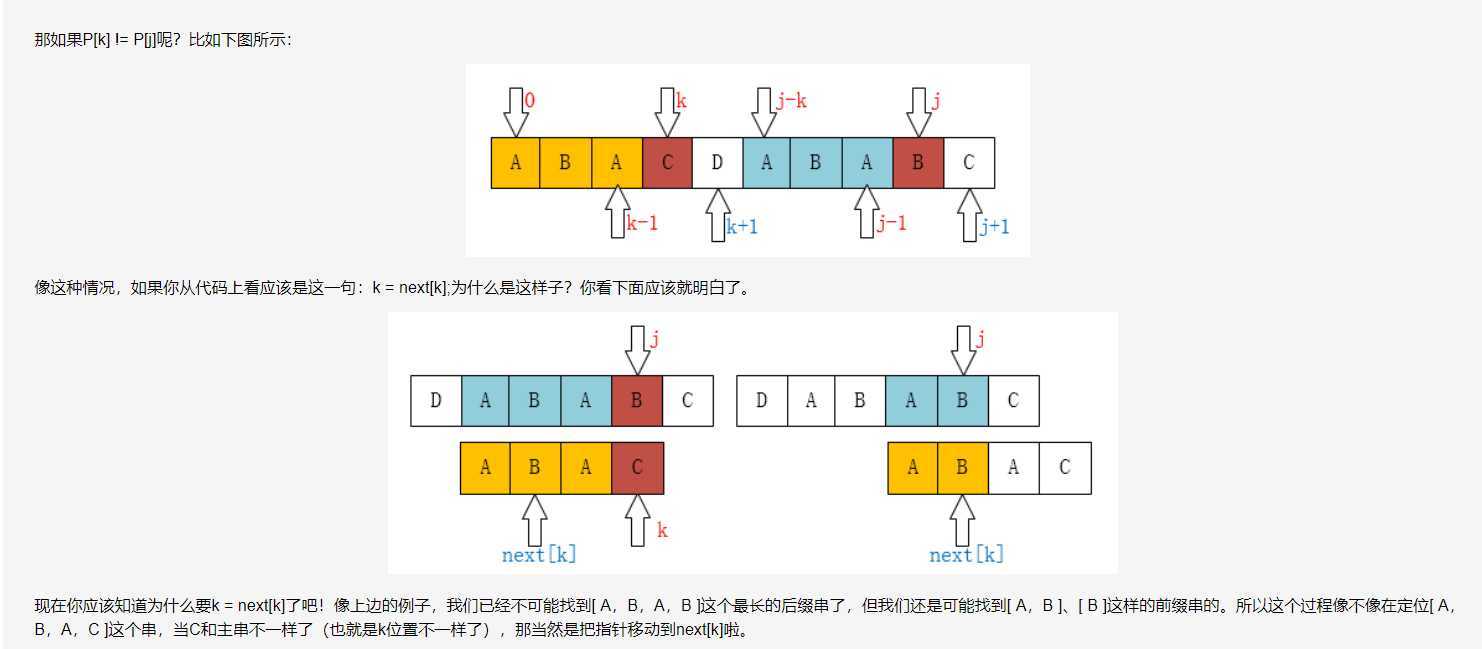
首先明确next数组作用,设T为主串,P为模式串(即为关键字),next数组作用为,当T[i] != P[j]后,模式串指针 j 应该回退到next[j]位置。
如果阅读过我说的这篇博客,就已经知道为什么指针 j 不用回退到0而要回退到next[j],因为要充分利用已经匹配的字符和模式串的特征来减少模式串指针回退,以降低时间复杂度。
求解next数组的代码如下:
1 void getNext(int next[], string p)
2 {
3 int j = 0, k = -1;
4 next[0] = -1;
5 while (j < p.size() - 1) {
6 if (k == -1 || p[j] == p[k]) {
7 j++;
8 k++;
9 next[j] = k;
10 } else
11 k = next[k];
12 }
13 }
其实我们可以将KMP算法理解成两次字符串匹配的过程,第一次发生在求next数组过程中,就是模式串P的最长前缀子串和最长后缀子串进行匹配的过程中,其中模式串是前缀子串,主串是后缀子串,模式串和主串都在同一个字符串中,如果模式串P[k] != P[j]时,模式串指针k自然要进行回退,回退到next[k]位置;第二次当然是模式串和主串的匹配过程,其中主串是T,模式串是P,当T[i] != P[j]时,模式串指针 j 进行回退,回退到next[j]位置。
在将KMP算法理解成两次匹配过程后,next[j]数组含义就是这篇博客提到的,模式串的前缀子串集和后缀子串集的最长相同元素,也就是目前在 j 位置之前最长前缀子串和最长后缀子串已经匹配字符的个数。如果肉眼去寻找这个结果是很简单的。
补充:前缀子串和后缀子串概念
前缀子串:从字符串头开始的子串。例如字符串:abcdef那么它的前缀子串为:a,ab,abc,abcd,最长的前缀子串便为 abcde;
后缀子串: 从字符串尾开始的子串。还是拿字符串abcdef举栗子它的后缀子串为:f,ef,def,最长的后缀子串便为 bcdef。
例如求模式串"ABACDABABC"的next的数组,此时的最长前缀子串为"ABACDABAB"作为模式串,最长后缀子串为"BACDABABC"作为主串(换一种说法,就是在最长后缀子串中寻找最长前缀子串)。
当P[k] == P[j]时,如下图:
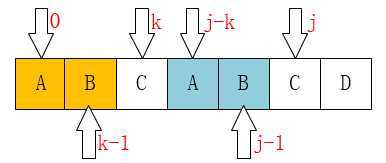
已经匹配了"ABC",j + 1位置的之前最长前缀子串和最长后缀子串匹配个数就是 k + 1 = 2 + 1 = 3(k从0开始,所以需要加1),对应代码 7~9行:
j++;
k++;
next[j] = k;
当P[k] != P[j]时,如下图,作为模式串的最长前缀子串的k指针应该回退,回退到什么位置呢?
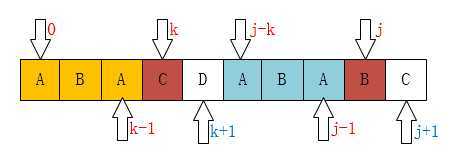
显然根据已经求出的next数据,就可以知道k应该回退到什么地方,k应该回退到next[k]位置,next[3] = 1,也就是k重新回到1位置,因为P[0 ~ next[k] - 1]已经和P[j - next[k] ~ j - 1]已经匹配,k指针只需要回退到next[k]位置再开始匹配即可,对应求next数组的第11行代码如下:
k = next[k];
最后处理两种特殊情况:
当next数组下标为0时,next[0] = -1, 放在第一次匹配过程中理解就是,当P[0] != P[j]时,k因该回退到-1,重新开始匹配过程;放在第二次匹配过程中理解就是,当P[0] != T[i]时,j 回退到-1,重新开始匹配过程。
当next数组下标为1时,next[1] = 0,放在第一次匹配过程中理解就是,当P[1] != P[j]时,k因该回退到0,从头开始开始匹配;放在第二次匹配过程中理解就是,当P[1] != T[i]时,j 回退到0,从头开始开始匹配。
改进求next数组方法:
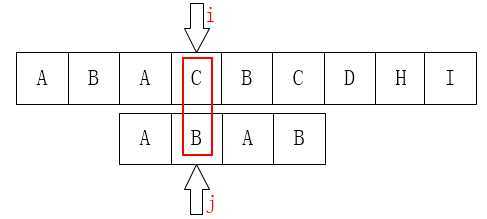
上边求next数据的方法有缺陷,当模P[j] != T[i]时(无论是第一次还是第二次匹配过程都有,只不过第一次求next匹配过程的模式串和主串都在同一个字符串中)会存在模式串指针 j 不能一次性回退到位的情况,当出现如下图情况时
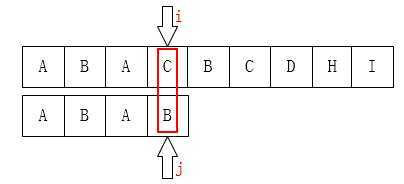
按照第一种求next数组方法j 应该回退到1,如下图哦所示,但是当回退到1时,还是会出现P[j] != T[i]的情况,因为A后面跟的都是B,所以应当让 j 直接回退到next[1] = 0。
所以改变后代码如下,改变在9~12行,在求next数组匹配过程中,当P[k] == P[j]或者k == 1时,并且P[k + 1] == P[j + 1]时,next[j + 1] == next[k + 1]
1 void getNext2(int next[], string p)
2 {
3 int j = 0, k = -1;
4 next[0] = -1;
5 while (j < p.size() - 1) {
6 if (k == -1 || p[j] == p[k]) {
7 j++;
8 k++;
9 if (p[j] == p[k])
10 next[j] = next[k];
11 else
12 next[j] = k;
13 } else
14 k = next[k];
15 }
16 }
原文:https://www.cnblogs.com/HyattXia/p/13401408.html