题解 HDU3686 【Traffic Real Time Query System】

P.S.此题无代码，只有口胡，因为作者码炸了。

题目大意

给你一个有 \(n\) 个点， \(m\) 条边的无向图，进行 \(q\) 次询问，每次询问两个点 \(u\) \(v\)，输出两个点的之间的路径经过了几个割点。

题解

这是一道模板题，先考虑用 \(Tarjan\) 求出割点的位置，再选择缩点。由于我们要缩的是点双连通分量，所以与强连通分量和边双连通分量有所不同。正解好像是圆方树，但是作者这里使用的是自己口胡的一种方法（一直过不了可能就是因为它，但是找不出错）。

对于这样的一个图，我们不像其他的点双连同分量一样缩点，将割点归于周围的点双连同分量，而是将割点与其相连的边断开，如下图：

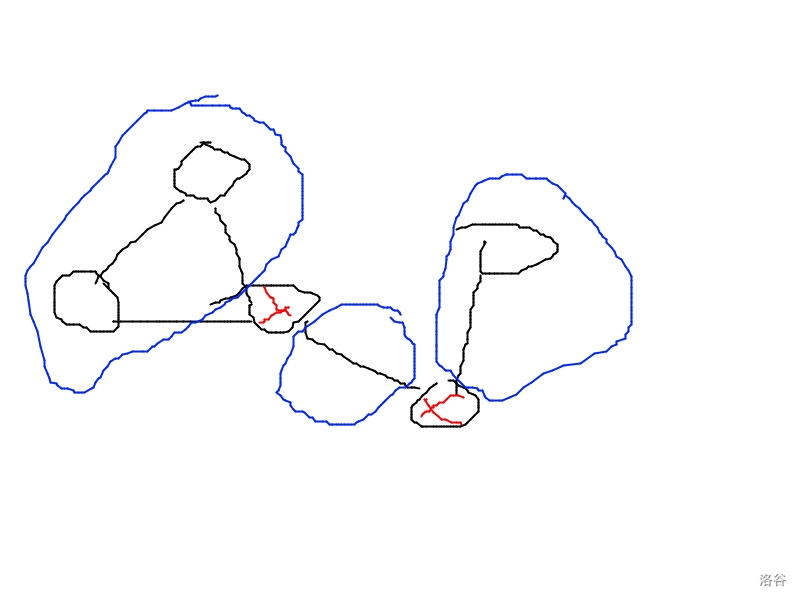
每一个点双连同分量最后形成的连同块都是不包括割点的，但是包括连向割点的边，这一步骤我们可以通过 \(DFS\) 完成，还是容易的。

错误代码（思路大概是没问题的，大家可以先看看）：

    for(int i=1;i<=n;++i)
    {
        if(!dfn[i])
        tarjan(i,i);//找割点
    }
    for(int i=1;i<=n;++i)
    {
        if(cut[i])
        {
            bel[i]=++len;//割点自己作为独立的点
            dis[len]=1;//割点对于答案的贡献
        }
        if(cut[i]||vis[i])
        continue;
        vis[i]=true;
        bel[i]=++len;
        dfs1(i,len);//标记加tag，点和边都要
    }
    for(int i=1;i<=m;++i)//建图
    {
        if(cut[u[i]]&&cut[v[i]])
        {
            tag[i]=++len;
            add(bel[u[i]],len);
            add(len,bel[u[i]]);
            add(bel[v[i]],len);
            add(len,bel[v[i]]);
            fa[find(bel[v[i]])]=len;
            fa[find(bel[u[i]])]=len;
            fa[len]=len;
            continue;
        }
        int fu=find(bel[u[i]]),fv=find(bel[v[i]]);//用并查集维护联通性
        if(fu!=fv)
        {
            add(bel[u[i]],bel[v[i]]);
            add(bel[v[i]],bel[u[i]]);
            fa[fu]=fv;
        }
    }

缩点完成了之后，这幅图就变成了森林（不保证图联通），然后我们可以愉快地用 \(DFS\) 统计任意一点到根的答案，然后跑树上 \(LCA\) ，用容斥原理统计答案。

错误代码如下:

    for(int i=1;i<=Q;++i)
    {
        scanf("%d%d",&x,&y);
        printf("%d\n",dis[tag[x]]+dis[tag[y]]-dis[tmp]-dis[to[tmp][0]]);
    }

题解 HDU3686 【Traffic Real Time Query System】

原文：https://www.cnblogs.com/Point-King/p/13405819.html