在OpenGL中,指定三角形图元的顶点顺序很重要。譬如,我们可以使用glFrontFace来指定顺时针还是逆时针为正面,然后通过glCullFace来cull掉背面或者正面.
但你有没有想过,OpenGL是怎么判断三角形的顶点顺序是顺时针还是逆时针呢?
首先我们先明确一下,culling这个阶段发生在viewport transformation之后,rasterization之前. 三维顶点经过MVP变换->透视除法->clipping->viewport transformation,得到的是屏幕坐标系下的二维顶点.
这样事情变得稍微简单了一些,我们只需要考虑三个二维顶点的顺序.
多边形的面积公式为:\(a = \frac{1}{2}\sum_{i=0}^{n-1}x_{i}y_{i\oplus 1} - x_{i\oplus 1}y_{i}\)
其中 \(i\oplus 1\) 表示 \((i+1)\) mod \(n\),用C语言描述:(i+1)%n.
将此公式应用到三角形,得:\(a = \frac{1}{2}(x_{0}y_{1} - x_{1}y_{0} + x_{1}y_{2} - x_{2}y_{1} + x_{2}y_{0} - x_{0}y_{2})\),作图来解释一下这个公式.
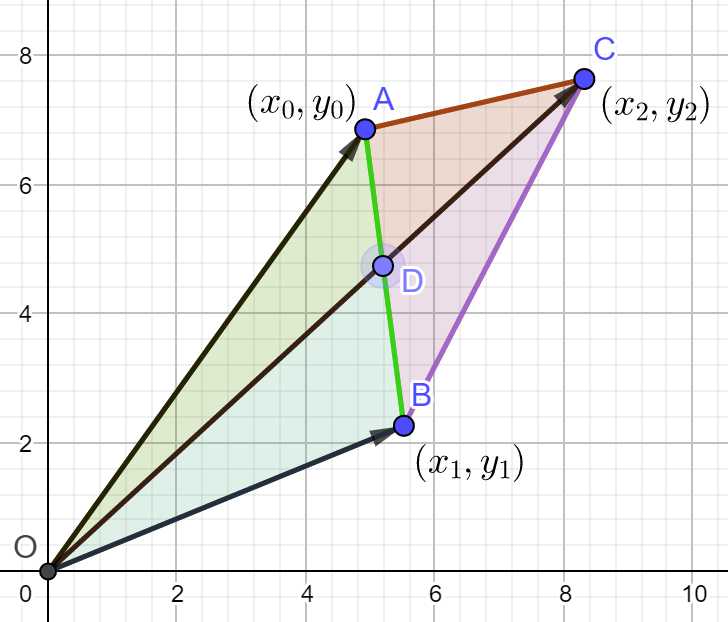
如图所示,\(\Delta ABC\)的面积,可以看作\(\Delta AOC\)的面积加上\(\Delta BOC\)的面积,然后减掉\(\Delta AOB\)的面积. 即:
\(S_{\Delta ABC} = -S_{\Delta AOB} + S_{\Delta BOC} + S_{\Delta AOC}\)
而三角形的面积恰恰是两条邻边向量叉乘的一半(带有正负号). 故有:
\(-S_{\Delta AOB} = \frac{1}{2}(\vec{OA} \times \vec{OB}) = \frac{1}{2}(x_{0}y_{1} - x_{1}y_{0})\)
\(S_{\Delta BOC} = \frac{1}{2}(\vec{OB} \times \vec{OC}) = \frac{1}{2}(x_{1}y_{2} - x_{2}y_{1})\)
\(S_{\Delta AOC} = \frac{1}{2}(\vec{OC} \times \vec{OA}) = \frac{1}{2}(x_{2}y_{0} - x_{0}y_{2})\)
将三者相加,就相当于四边形\(OBCA\)的面积减去\(\Delta AOB\)的面积,恰好就是\(\Delta ABC\)的面积,且这个面积是正的. 图示的三角形是顶点顺序是逆时针顺序. 同学们可以自行验证一下. 把顺序变成顺时针时,得到的面积是逆时针的相反数.
所以通过三角形面积的正负号判断其顶点顺序是可行的.
凸多边形应用上述公式也是可行的,在此不再赘述. 下面我们主要看一下凹多边形的面积是否也能满足此公式.
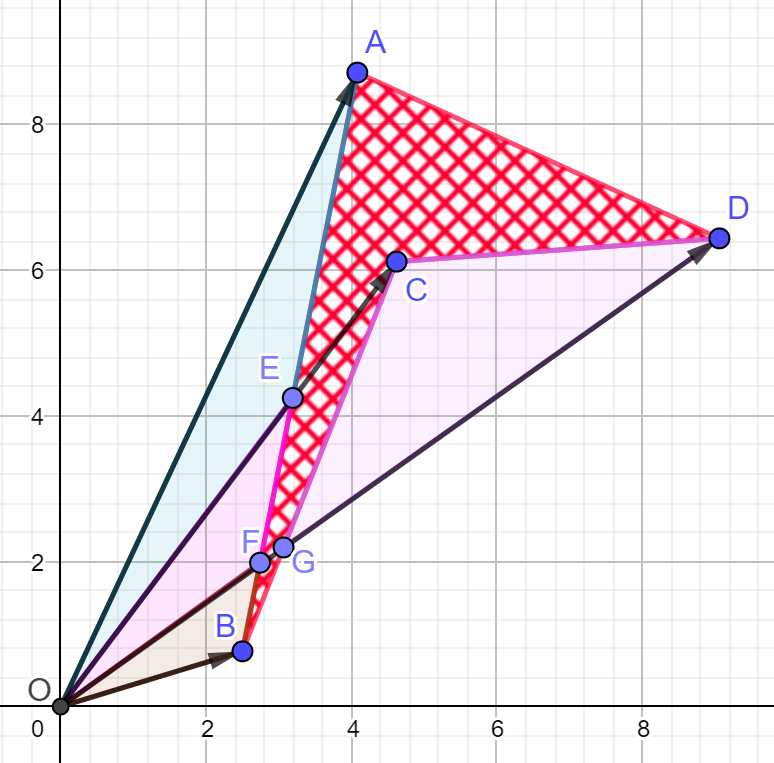
我们求的是凹多边形\(ABCD\)的面积. 纯色的三角形面积总能被公式叉乘运算的两个三角形面积抵消掉. 例如\(S_{\Delta FOB}\)可以通过\(S_{\Delta AOB}\)和\(S_{\Delta OBC}\)抵消掉,\(S_{\Delta CGD}\)可以通过\(S_{\Delta ODA}\)和\(S_{\Delta ODC}\)抵消掉. 最后得到的就是凹多边形的面积.
原文:https://www.cnblogs.com/howelldong/p/13413259.html