斐波那契

斐波那契(fibonacci)( \(\star\star?\))

• 时限：\(1s\) 内存：\(256M\)

Descrption

• 小 \(C\) 养了一些很可爱的兔子。

• 有一天，小 \(C\) 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行繁衍：一对兔子从出生后第二个月起，每个月刚开始的时候都会产下一对小兔子。我们假定，在整个过程中兔子不会出现任何意外。

• 小 \(C\) 把兔子按出生顺序，把兔子们从 \(1\) 开始标号，并且小 \(C\) 的兔子都是 \(1\) 号兔子和 \(1\)号兔子的后代。如果某两对兔子是同时出生的，那么小 \(C\) 会将父母标号更小的一对优先标号。

• 如果我们把这种关系用图画下来，前六个月大概就是这样的：

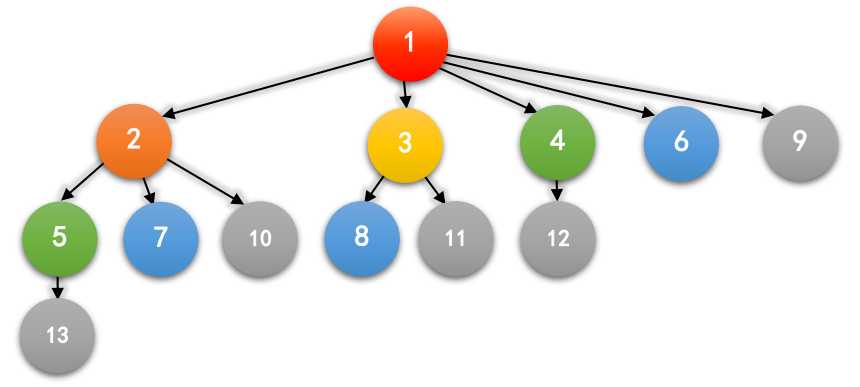
• 其中，一个箭头\(A\)→\(B\)表示\(A\)是\(B\)的祖先，相同的颜色表示同一个月出生的兔子。

• 为了更细致地了解兔子们是如何繁衍的，小 \(C\) 找来了一些兔子，并且向你提出了\(m\)个问题：她想知道关于每两对兔子\(a_i\)和\(b_i\)，他们的最近公共祖先是谁。你能帮帮小 \(C\) 吗？

• 一对兔子的祖先是这对兔子以及他们父母（如果有的话）的祖先，而最近公共祖先是指两对兔子所共有的祖先中，离他们的距离之和最近的一对兔子。比如，\(5\) 和 \(7\) 的最近公共祖先是 \(2\)，\(1\) 和 \(2\) 的最近公共祖先是 \(1\)，\(6\) 和 \(6\) 的最近公共祖先是 \(6\)。

Input

• 输入第一行，包含一个正整数\(m\)。
  输入接下来m行，每行包含 2 个正整数，表示\(a_i\)和\(b_i\)。

Output

• 输入一共\(m\)行，每行一个正整数，依次表示你对问题的答案。

Sample Input

5
1 1
2 3
5 7
7 13
4 12

Sample Output

1
1
2
2
4

Hint

• 子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。
  每个测试点的数据规模及特点如下表：

  

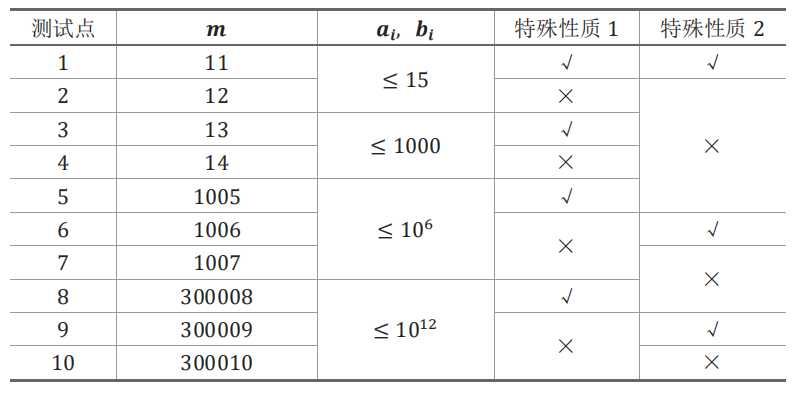
• 特殊性质 1：保证\(a_i,b_i\)均为某一个月出生的兔子中标号最大的一对兔子。例如，对于前六个月，标号最大的兔子分别是 1, 2, 3, 5, 8, 13。

• 特殊性质 2：保证\(|a_i-b_i|\leq 1\)。

• 来源：

分析

• 此题很有意思，我们从编号为 \(2\) 的兔子开始，依次写出他们的父亲节点的编号：
  • \(1,1,1,2,1,2,3,1,2,3,4,5,...\)
• 我们发现上面序列是有一段段连续的从 \(1\) 开始的序列组成的，序列长度为：
  • \(1,1,2,3,5,8,...\)
• 正好为斐波拉切数列，我们令 \(f[i]\) 表示第 \(i\) 个月的兔子数，显然 \(f[i]=f[i-1]+f[i-1]\) 。即第 \(i\) 个月的兔子数等于第 \(i-1\) 个月的兔子数 \(+\) 新出生的兔子数，而第 \(i-2\) 个月的所有兔子都会生出一个兔子。所以第 \(i\) 个月出生的兔子父亲编号依次为 \(1\sim f[i-2]\) 。
• 如果兔子编号为 \(x\) ,如果我能求出这只兔子是当月出生的第几只兔子，我们就能直到它的父亲节点是谁。假设\(f[i]< x < f[i+1]\) ，显然 \(x\) 是第 \(i+1\) 月第 \(x-f[i]\) 只出生的兔子，即 \(x\) 的父亲节点为 \(x-f[i]\) 。
• 显然 \(f[i]\) 是一个单调递增序列，通过二分，我们很容易找到小于等于 \(x\) 的 \(f[i]\) ,这也就找到了 \(x\) 的父亲节点。
• \(a_i,b_i \le 10^{12}\) ，显然这是无法建树的，首先数组就开不了，大概 \(60\) 个月后，兔子数会超过 \(10^{12}\)
• 对于特殊性质 \(1\) 刚好：\(father[f[i]]=f[i-2]\)，所以顺着往上推即可。
• 对于特殊性质 \(2\) ：\(lca(i,i)=i,lca(i,i+1)=1\)。
• 其他的情况我们可以对编号大的二分找到其是哪个月第几个出生的兔子，找到其父节点，判断与另一点是否相同，在往上找的过程中如果满足性质 \(1\) 或 \(2\) ，依照上面分析进行即可。

斐波那契

原文：https://www.cnblogs.com/hbhszxyb/p/13425626.html